题目内容
 如图,△ABC内接于⊙O,外角∠BAM的平分线与⊙O交于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①AE=AF;②
如图,△ABC内接于⊙O,外角∠BAM的平分线与⊙O交于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①AE=AF;② ;③BE=CF;④DF为⊙O的切线.其中正确的是
;③BE=CF;④DF为⊙O的切线.其中正确的是
- A.①②④
- B.②③④
- C.①③④
- D.①②③
D
分析:根据HL定理以及外角的性质和圆心角定理,分别进行判断即可得出答案.
解答: 解:连接BD,CD,
解:连接BD,CD,
∵△ABC内接于⊙O,外角∠BAM的平分线与⊙O交于点D,DE⊥AB于点E,DF⊥AC于点F,
∴DF=DE,
∵在Rt△ADF和Rt△ADE中,
 ,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AE=AF,
故①正确;
∵∠ABC+∠ACB=∠BAF,
∠BAD=∠DAF,
∴∠BAD= (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴ =
=
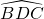 ,
,
∴② ,故②正确;
,故②正确;
∵ ,
,
∴BD=CD,
∵DE=DF,
在Rt△CDF和Rt△BDE中,
 ,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,故③正确;
无法证明DF为⊙O的切线,故④选项错误,
故①②③正确,
故选:D.
点评:此题主要考查了角平分线的性质以及全等三角形的判定等知识,根据已知得出∠BAD= (∠ABC+∠ACB)进而得到
(∠ABC+∠ACB)进而得到 是解题关键.
是解题关键.
分析:根据HL定理以及外角的性质和圆心角定理,分别进行判断即可得出答案.
解答:
 解:连接BD,CD,
解:连接BD,CD,∵△ABC内接于⊙O,外角∠BAM的平分线与⊙O交于点D,DE⊥AB于点E,DF⊥AC于点F,
∴DF=DE,
∵在Rt△ADF和Rt△ADE中,
 ,
,∴Rt△ADF≌Rt△ADE(HL),
∴AE=AF,
故①正确;
∵∠ABC+∠ACB=∠BAF,
∠BAD=∠DAF,
∴∠BAD=
 (∠ABC+∠ACB),
(∠ABC+∠ACB),∴
 =
=
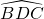 ,
,∴②
 ,故②正确;
,故②正确;∵
 ,
,∴BD=CD,
∵DE=DF,
在Rt△CDF和Rt△BDE中,
 ,
,∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,故③正确;
无法证明DF为⊙O的切线,故④选项错误,
故①②③正确,
故选:D.
点评:此题主要考查了角平分线的性质以及全等三角形的判定等知识,根据已知得出∠BAD=
 (∠ABC+∠ACB)进而得到
(∠ABC+∠ACB)进而得到 是解题关键.
是解题关键. 
练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.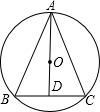 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.