题目内容
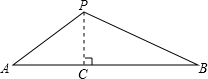
如图，在玉溪市聂耳广场上空有一盏孔明灯P，A、B是地面上相距90米的两点，它们分别在正西和正东向上，测得仰角∠PAB=45°，仰角∠PBA=30°．求孔明灯P的高度．（精确到0.1米，| 3 |
分析：过点P作PC⊥AB于C点，由PC及∠A、∠B的正切值表示出AB，即AB=
+
，求得PC即可．
| PC |
| tan∠A |
| PC |
| tan∠B |
解答：解：如图：过点P作PC⊥AB于C点，
设PC=x米，
在Rt△PAC中，tan∠PAB=
，
∴AC=
=PC=x（米），
在Rt△PBC中，tan∠PBA=
，
∴BC=
=
x（米），
又∵AB=90，
∴AB=AC+BC=x+
x=90，
∴x=
=45(
-1)（米）．
∴PC=45（1.732-1）=32.9（米）．
答：孔明灯P的高度约为32.9米．
设PC=x米，在Rt△PAC中，tan∠PAB=
| PC |
| AC |
∴AC=
| PC |
| tan45° |
在Rt△PBC中，tan∠PBA=
| PC |
| BC |
∴BC=
| PC |
| tan30° |
| 3 |
又∵AB=90，
∴AB=AC+BC=x+
| 3 |
∴x=
| 90 | ||
1+
|
| 3 |
∴PC=45（1.732-1）=32.9（米）．
答：孔明灯P的高度约为32.9米．
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
正东向上，测得仰角∠PAB=45°，仰角∠PBA=30°．求孔明灯P的高度．（精确到0.1米，
=1.732）
=1.732）
=1.732）
=1.732）