题目内容
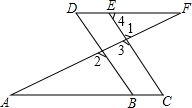
如图:AF,BD,CE是直线,B在直线AC上,E在直线DF上,∠A=∠F,∠C=∠D.说明∠1与∠2相等的理由.
解:因为∠A=∠F(已知),
所以
所以
因为∠C=∠D(已知),
所以
所以
所以∠2=∠3
因为∠1=∠3
所以∠1=∠2( 等量代换).

解:因为∠A=∠F(已知),
所以
DF
DF
∥AC
AC
.所以
∠C=∠4
∠C=∠4
.因为∠C=∠D(已知),
所以
∠4=∠D
∠4=∠D
(等量代换).所以
EC
EC
∥BD
BD
.所以∠2=∠3
两直线平行,同位角相等
两直线平行,同位角相等
.因为∠1=∠3
对顶角相等
对顶角相等
,所以∠1=∠2( 等量代换).
分析:利用平行线的判定定理,首先根据内错角相等,两直线平行,证得DF∥AC,然后利用平行线的性质以及等量代换,证得:∠4=∠D,则EC∥BD,再利用平行线的性质以及等量代换即可证得∠1=∠2.
解答:解:因为∠A=∠F(已知),
所以 DF∥AC.
所以∠C=∠4.
因为∠C=∠D(已知),
所以∠4=∠D(等量代换).
所以 EC∥BD.
所以∠2=∠3 两直线平行,同位角相等.
因为∠1=∠3 对顶角相等,
所以∠1=∠2( 等量代换).

所以 DF∥AC.
所以∠C=∠4.
因为∠C=∠D(已知),
所以∠4=∠D(等量代换).
所以 EC∥BD.
所以∠2=∠3 两直线平行,同位角相等.
因为∠1=∠3 对顶角相等,
所以∠1=∠2( 等量代换).
点评:本题考查了平行线的性质定理以及判定定理,正确认识定理是解题的关键.

练习册系列答案
相关题目
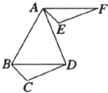 14、如图,AF∥BD,AE∥BC,且AF=BD,AE=BC,则线段EF是通过平移线段
14、如图,AF∥BD,AE∥BC,且AF=BD,AE=BC,则线段EF是通过平移线段