题目内容
15.先化简:$\frac{{m}^{2}}{m-1}$-$\frac{1-2m}{1-m}$,再选取一个适当的m的值代入求值.分析 先把分母化为同分母,再进行同分母的减法运算,接着把分之分解后约分得到原式=m-1,然后取m=2016求分式的值.
解答 解:原式=$\frac{{m}^{2}}{m-1}$-$\frac{2m-1}{m-1}$
=$\frac{{m}^{2}-2m+1}{m-1}$
=$\frac{(m-1)^{2}}{m-1}$
=m-1,
当m=2016时,原式=2016-1=2015.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
6.下列说法正确的是( )
| A. | “购买1张彩票就中奖”是不可能事件 | |
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
3.下列命题中,是假命题的是( )
| A. | 对顶角相等 | |
| B. | 同旁内角互补 | |
| C. | 两点确定一条直线 | |
| D. | 角平分线上的点到这个角的两边的距离相等 |
20. 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )| A. | 70° | B. | 80° | C. | 110° | D. | 120° |
4.下列命题中错误的是( )
| A. | 平行四边形的对角线互相平分 | B. | 菱形的对角线互相垂直 | ||
| C. | 同旁内角互补 | D. | 矩形的对角线相等 |
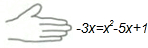 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图: