题目内容
如图1,等腰梯形ABCD,AD∥BC,AB=DC=AD=4cm.∠ABC=60°.
(1)求梯形ABCD的面积;
(2)过B作直线EF⊥BC于B(如图2),直线EF右点B开始,沿射线BC向右以1cm/s的速度运动,在运动过程中,始终保持EF⊥BC,设运动时间为t秒,梯形ABCD在直线EF左侧部分的面积为Scm2,求S与t的函数关系式,并写出相应的自变量t的取值范围.
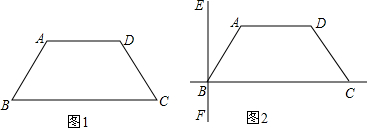
(1)求梯形ABCD的面积;
(2)过B作直线EF⊥BC于B(如图2),直线EF右点B开始,沿射线BC向右以1cm/s的速度运动,在运动过程中,始终保持EF⊥BC,设运动时间为t秒,梯形ABCD在直线EF左侧部分的面积为Scm2,求S与t的函数关系式,并写出相应的自变量t的取值范围.

分析:(1)过A作AE⊥BC于E,过D作DF⊥BC于F,得出四边形AEFD是矩形,推出AD=EF,AE=DF,求出BE,AE,根据梯形面积公式求出即可.
(2)分为四种情况::①当0≤t≤2时,②当2<t≤6时,③当6<t<8时,④当t≥8时,根据梯形和三角形面积求出即可.
(2)分为四种情况::①当0≤t≤2时,②当2<t≤6时,③当6<t<8时,④当t≥8时,根据梯形和三角形面积求出即可.
解答: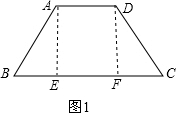 解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F,
解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F,
则AE∥DF,∠AEB=∠DFC=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF,AE=DF,
∵AB=DC,
∴在Rt△AEB和Rt△DFC中,由勾股定理得:BE=FC,
∵∠B=60°,
∴∠BAE=30°
∴BE=
AB=
×4cm=2cm,由勾股定理得:AE=2
cm,
∴CF=2cm,
∴BC=2+4+2=8(cm),
∴梯形ABCD的面积是
(AD+BC)×AE=
×(4cm+8cm)×2
cm=12
cm2.
(2)分为四种情况:
①当0≤t≤2时,如图2,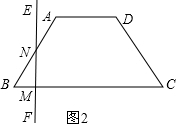 BM=t
BM=t
∵∠NMB=90°,∠B=60°,
∴MN=
t,
S=
•t•
t=
t2,
即S=
t2,自变量t的范围是0≤t≤2;
②当2<t≤6时,如图3,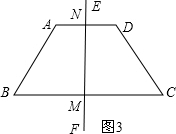 BM=t,
BM=t,
由(1)知:AN=t-2,MN=2
,
则S=
×(AN+BM)×MN
=
•(t-2+t)•2
,
即S=2
t-2
,自变量t的范围是2<t≤6;
③当6<t<8时,如图4, CM=8-t
CM=8-t
∵四边形ABCD是等腰梯形,∠B=60°,
∴∠C=∠B=60°,
∴MN=
CM=(8-t)
,
S=S梯形ABCD-S△CMN=12
-
(8-t)•
(8-t),
即S=-
t2+8
t-20
,自变量t的范围是6<t<8;
④当t≥8时,S=S梯形ABCD=12
,
即S=12
,自变量t的范围是t≥8.
 解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F,
解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F,则AE∥DF,∠AEB=∠DFC=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF,AE=DF,
∵AB=DC,
∴在Rt△AEB和Rt△DFC中,由勾股定理得:BE=FC,
∵∠B=60°,
∴∠BAE=30°
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴CF=2cm,
∴BC=2+4+2=8(cm),
∴梯形ABCD的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)分为四种情况:
①当0≤t≤2时,如图2,
 BM=t
BM=t∵∠NMB=90°,∠B=60°,
∴MN=
| 3 |
S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
即S=
| ||
| 2 |
②当2<t≤6时,如图3,
 BM=t,
BM=t,由(1)知:AN=t-2,MN=2
| 3 |
则S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
即S=2
| 3 |
| 3 |
③当6<t<8时,如图4,
 CM=8-t
CM=8-t∵四边形ABCD是等腰梯形,∠B=60°,
∴∠C=∠B=60°,
∴MN=
| 3 |
| 3 |
S=S梯形ABCD-S△CMN=12
| 3 |
| 1 |
| 2 |
| 3 |
即S=-
| ||
| 2 |
| 3 |
| 3 |
④当t≥8时,S=S梯形ABCD=12
| 3 |
即S=12
| 3 |
点评:本题考查了等腰梯形的性质,矩形的性质和判定,勾股定理,含30度角的直角三角形性质,三角形的面积的应用,题目综合性比较强,用了分类讨论思想.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 1、如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=AB.点E,F分别在AD,AB上,AE=BF,DF与CE相交于P,则∠DPE=
1、如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=AB.点E,F分别在AD,AB上,AE=BF,DF与CE相交于P,则∠DPE= (2005•闸北区二模)已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:
(2005•闸北区二模)已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证: (2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=(
(2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=( 点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒:
点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒:
