题目内容
如图,在等腰梯形ABCD中,M、N分别为AD、BC的中点,E、F分别为BM、CM的中点。
(1)求证:△ABM≌△CDM;
(2)判断并证明四边形MENF是何种特殊的四边形;
‚当等腰梯形ABCD的高h与底边BC满足怎样的数量关系时,四边形MENF是正方形?(直接写出结论,不需要证明).
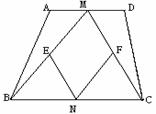
(1)∵ABCD为等腰梯形,
∴AB=CD,∠A=∠D,
又∵M为AD的中点,
∴MA=MD.
∴△AMB≌△DMC, 3分
(2)判断四边形MENF为菱形; 1分
由(1)得△AMB≌△DMC,
∴BM=CM;
又∵E、F、N分别为BM、CM、BC中点,
∴MC=2MF=2NE,BM=2ME=2NF,(或MF∥NE,ME∥NF;)
∴EM=NF=MF=NE; 4
∴四边形MENF为菱形.
(说明:第(2)问判断四边形MENF仅为平行四边形,并正确证明的只给(2分).)
‚当BC=2h或BC=2MN时,MENF为正方形.(2分)

练习册系列答案
相关题目
由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是( )

|
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 ﹣1)0﹣
﹣1)0﹣ .
. ,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子
,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子 有意义,则x>1;⑤在反比例函数
有意义,则x>1;⑤在反比例函数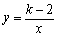 中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( )
中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( ) ,0),B(
,0),B(

 ”,小明做了下列三个模拟实验来验证。
”,小明做了下列三个模拟实验来验证。
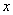 米,试将△EMN的面积S(平方米)表示成关于x的函数;
米,试将△EMN的面积S(平方米)表示成关于x的函数;