Question

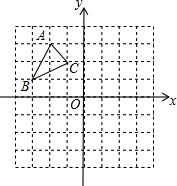如图，△ABC中A（-2，3），B（-3，1），C（-1，2）．
（1）△ABC将各点的横坐标增加4个单位长度，纵坐标保持不变，得△A₁B₁C₁，画出△A₁B₁C₁（记为“1”）；
（2）将△ABC各点的横坐标保持不变，纵坐标分别乘-1，得△A₂B₂C₂，画出△A₂B₂C₂（记为“2”）；
（3）将△A₂B₂C₂各点的纵坐标保持不变，横坐标分别乘以-1，得△A₃B₃C₃，画出△A₃B₃C₃（记为“3”）；
（4）在“1”、“2”、“3”中，______与______（填数字记号）成轴对称，对称轴是______；______与______（填数字记号）成中心对称，对称中心的坐标是______．
（5）平面直角坐标系内将一个点P（a，b）绕坐标原点逆时针旋转90°，结合图形观察变换前后对应点坐标的关系，写出P的对应点P′的坐标为______．

Answer 1

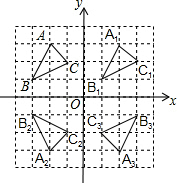解：（1）如图所示，△A₁B₁C₁即为所求．
（2）如图所示，△A₂B₂C₂即为所求．
（3）如图所示，△A₃B₃C₃即为所求．
（4）由图可知，2与 3（填数字记号）成轴对称，对称轴是 y轴； 1与 3（填数字记号）成中心对称，对称中心的坐标是 （2，0）．
（5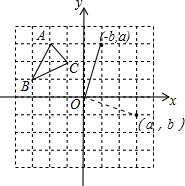）如图：P的对应点P′的坐标为（-b，a）．








故答案为：2，3，y轴，1，3，（2，0），（-b，a）．
分析：（1）分别求出△ABC将各点的横坐标增加4个单位长度，纵坐标保持不变时A₁、B₁、C₁的坐标，画出△A₁B₁C₁即可；
（2）先求出△ABC各点的横坐标保持不变，纵坐标分别乘-1后A₂、B₂、C₂的坐标，画出△A₂B₂C₂即可；
（3）将△A₂B₂C₂各点的纵坐标保持不变，横坐标分别乘以-1，A₃、B₃、C₃的坐标，画出△A₃B₃C₃即可；
（4）分别根据轴对称及中心对称的性质进行解答即可；
（5）根据点（a，b）绕原点逆时针旋转90°得到的坐标为（-b，a）解答即可．
点评：本题考查了旋转变换与轴对称变换，画出图形是解题的关键．