题目内容
如图,足球上守门员在O处开出一高球.球从离地面1米的A处飞出(A在y轴上),把球看成点.其运行的高度y(单位:m)与运行的水平距离x(单位:m)满足关系式y=a(x﹣6)2+h.
(1)①当此球开出后.飞行的最高点距离地面4米时.求y与x满足的关系式.
②在①的情况下,足球落地点C距守门员多少米?(取4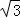 ≈7)
≈7)
③如图所示,若在①的情况下,求落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.求:站在距O带你6米的B处的球员甲要抢到第二个落点D处的求.他应再向前跑多少米?(取2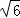 =5)
=5)
(2)球员乙升高为1.75米.在距O点11米的H处.试图原地跃起用头拦截.守门员调整开球高度.若保证足球下落至H正上方时低于球员乙的身高.同时落地点在距O点15米之内.求h的取值范围.
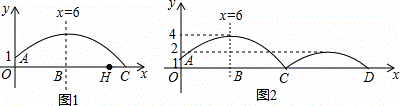
考点: 二次函数的应用.
分析: (1)①由飞行的最高点距离地面4米,可知h=4,又A(0,1)即可求出解析式;
②令y=0,解方程即可解决问题;
③如图2所示,根据CD=EF,要求CD只要求出EF,又足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,可知此时y=2,解方程求出E、F的横坐标,求出EF可解决问题;
(2)由A(0,1)代入y=a(x﹣6)2+h,得到a= ,由x=11和x=15,求出y列不等式组即可.
,由x=11和x=15,求出y列不等式组即可.
解答: 解:(1)①当h=4时,y=a(x﹣6)2+4,又A(0,1)
∴1=a(0﹣6)2+4,
∴a=﹣ ,
,
∴y=﹣ (x﹣6)2+4;
(x﹣6)2+4;
②令y=0,则0=﹣ (x﹣6)2+4,解得:x1=4
(x﹣6)2+4,解得:x1=4 +6≈13,x2=﹣4
+6≈13,x2=﹣4 +6<0(舍去)
+6<0(舍去)
∴足球落地点距守门员约13米;
③如图,第二次足球弹出后的距离为CD,根据题意,CD=EF,
又足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,
∴2=﹣ (x﹣6)2+4,
(x﹣6)2+4,
解得:x1=6﹣2 ,x2=6+2
,x2=6+2 ,
,
∴CD=EF=|x1﹣x2|=4 ≈10,
≈10,
∴BD=13﹣6+10=17(米),
答:他应再向前跑17米;
(2)将x=0,y=1代入y=a(x﹣6)2+h,得a= ,
,
当x=11时,y= (11﹣6)2+h=
(11﹣6)2+h= ,
,
解 <1.75,得x<
<1.75,得x< ,
,
当x=15时,y= (15﹣6)2+h=
(15﹣6)2+h= ,
,
解 ≤0,得x≥
≤0,得x≥ ,
,
∴ ≤x<
≤x< .
.

点评: 本题主要考查了二次函数的实际应用,弄清题意,数形结合,把函数问题转化为方程或不等式问题是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出 部分频数分布表和部分频数分布直方图如图表:
部分频数分布表和部分频数分布直方图如图表:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 6 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 8 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则
本次测试的优秀率是多少?
(4)第5组8名同学中,有4名男同学,
现将这8名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小亮与小华两名男同学分在同一组的概率.

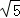 ,则tan∠CAD的值是( )
,则tan∠CAD的值是( )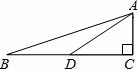
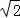 C.
C.  D.
D. 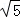
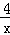 在第一象限的图象经过其顶点A,点D为斜边OA的中点,另一个反比例函数y1=
在第一象限的图象经过其顶点A,点D为斜边OA的中点,另一个反比例函数y1=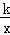 在第一象限的图象经过点D,则k的值为( )
在第一象限的图象经过点D,则k的值为( )
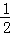 D. 无法确定
D. 无法确定


