题目内容
 (2011•德阳)如图,AB是⊙0的直径,AC切⊙0于点A,AD是⊙0的弦,OC⊥AD于F交⊙0于E,连接DE,BE,BD.AE.
(2011•德阳)如图,AB是⊙0的直径,AC切⊙0于点A,AD是⊙0的弦,OC⊥AD于F交⊙0于E,连接DE,BE,BD.AE.(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=
| 3 | 4 |
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
分析:(1)根据切线性质、垂直的性质、直角三角形的两个锐角互余的性质求得∠C+∠AOC=∠AOC+∠BAD=90°,即∠C=∠BAD;然后由圆周角定理推知∠BED=∠BAD;最后由等量代换证得∠C=∠BED;
(2)根据锐角三角函数的定义求AC的长;
(3)根据已知条件推知AE=BD=DE,然后由圆的弧、弦、圆心角间的关系知
=
=
,从而求得∠BAD=30°;然后由直径AB所对的圆周角∠ADB=90°可以求得直角三角形ABD中30°所对的直角边是斜边的一半BD=
AB=5,DE=5;最后(过点D作DH⊥AB于H)在直角三角形HDA中求得高线DH的长度,从而求得梯形ABDE的面积.
(2)根据锐角三角函数的定义求AC的长;
(3)根据已知条件推知AE=BD=DE,然后由圆的弧、弦、圆心角间的关系知
 |
| AE |
 |
| BD |
 |
| DE |
| 1 |
| 2 |
解答: (1)证明:∵AB是⊙O的直径,CA切⊙O于A,
(1)证明:∵AB是⊙O的直径,CA切⊙O于A,
∴∠C+∠AOC=90°;
又∵0C⊥AD,
∴∠OFA=90°,
∴∠AOC+∠BAD=90°,
∴∠C=∠BAD.
又∵∠BED=∠BAD,
∴∠C=∠BED.
(2)解:由(1)知∠C=∠BAD,tan∠BAD=
,
∴tan∠C=
.
在Rt△OAC中,tan∠C=
,且OA=
AB=5,
∴
=
,解得AC=
.
(3)解:∵OC⊥AD,∴
=
,∴AE=ED,
又∵DE∥AB,∴∠BAD=∠EDA,∴
=
,
∴AE=BD,
∴AE=BD=DE,
∴
=
=
,
∴∠BAD=30°,
又∵AB是直径,∴∠ADB=90°,
∴BD=
AB=5,DE=5,
在Rt△ABD中,由勾股定理得:AD=5
,
过点D作DH⊥AB于H,
∵∠HAD=30°,∴DH=
AD=
,
∴四边形AEDB的面积=
(DE+AB)•DH=
×(5+10)×
=
.
 (1)证明:∵AB是⊙O的直径,CA切⊙O于A,
(1)证明:∵AB是⊙O的直径,CA切⊙O于A,∴∠C+∠AOC=90°;
又∵0C⊥AD,
∴∠OFA=90°,
∴∠AOC+∠BAD=90°,
∴∠C=∠BAD.
又∵∠BED=∠BAD,
∴∠C=∠BED.
(2)解:由(1)知∠C=∠BAD,tan∠BAD=
| 3 |
| 4 |
∴tan∠C=
| 3 |
| 4 |
在Rt△OAC中,tan∠C=
| OA |
| AC |
| 1 |
| 2 |
∴
| 5 |
| AC |
| 3 |
| 4 |
| 20 |
| 3 |
(3)解:∵OC⊥AD,∴
 |
| AE |
 |
| ED |
又∵DE∥AB,∴∠BAD=∠EDA,∴
 |
| AE |
 |
| BD |
∴AE=BD,
∴AE=BD=DE,
∴
 |
| AE |
 |
| BD |
 |
| DE |
∴∠BAD=30°,
又∵AB是直径,∴∠ADB=90°,
∴BD=
| 1 |
| 2 |
在Rt△ABD中,由勾股定理得:AD=5
| 3 |
过点D作DH⊥AB于H,
∵∠HAD=30°,∴DH=
| 1 |
| 2 |
5
| ||
| 2 |
∴四边形AEDB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
75
| ||
| 4 |
点评:本题考查了圆周角定理、勾股定理、平行线的性质以及锐角三角函数的定义.解题时,注意知识的综合利用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•德阳)如图,在平面直角坐标系中,已知点A(a,0),B(0,b),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
(2011•德阳)如图,在平面直角坐标系中,已知点A(a,0),B(0,b),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )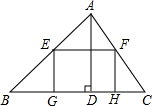 (2011•德阳)如图,有一块△ABC材料,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长l的取值范围是( )
(2011•德阳)如图,有一块△ABC材料,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长l的取值范围是( ) (2011•德阳)如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB=
(2011•德阳)如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB= (2011•德阳)如图,在直角三角形ABC中,∠C=90°,AC=12.BC=16,点0为△ABC的内心,点M为斜边AB的中点,则OM的长为
(2011•德阳)如图,在直角三角形ABC中,∠C=90°,AC=12.BC=16,点0为△ABC的内心,点M为斜边AB的中点,则OM的长为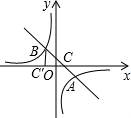 (2011•德阳)如图,已知一次函数y=-x+1与反比例函数
(2011•德阳)如图,已知一次函数y=-x+1与反比例函数