题目内容
（2011•德阳）如图，在△ABC中，AD⊥BC于D，如果BD=9，DC=5，cosB=| 3 |
| 5 |
| 12 |
| 13 |
| 12 |
| 13 |
分析：根据AD⊥BC于D，BD=9，cosB=
求得AB=15，由勾股定理得AD=12、AC=13，再利用直角三角形的性质求得∠EDC=∠ECD，从而利用sin∠EDC=sin∠ECD求解．
| 3 |
| 5 |
解答：解：∵AD⊥BC于D，BD=9，cosB=
，
∴AB=BD÷cosB=9×
=15，
∴由勾股定理得AD=12，
∵DC=5，
∴AC=13，
∵E为AC的中点，
∴ED=
AC=EC
∴∠EDC=∠ECD
∴sin∠EDC=sin∠ECD=
=
；
故答案为
．
| 3 |
| 5 |
∴AB=BD÷cosB=9×
| 5 |
| 3 |
∴由勾股定理得AD=12，
∵DC=5，
∴AC=13，
∵E为AC的中点，
∴ED=
| 1 |
| 2 |
∴∠EDC=∠ECD
∴sin∠EDC=sin∠ECD=
| AD |
| AC |
| 12 |
| 13 |
故答案为
| 12 |
| 13 |
点评：本题考查了解直角三角形、直角三角形斜边上的中线及勾股定理的知识，考查的知识点比较多且碎．
练习册系列答案
阅读快车系列答案
相关题目
（2011•德阳）如图，在平面直角坐标系中，已知点A（a，0），B（0，b），如果将线段AB绕点B顺时针旋转90°至CB，那么点C的坐标是（ ）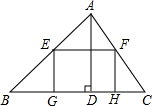
（2011•德阳）如图，有一块△ABC材料，BC=10，高AD=6，把它加工成一个矩形零件，使矩形的一边GH在BC上，其余两个顶点E，F分别在AB，AC上，那么矩形EFHG的周长l的取值范围是（ ）
（2011•德阳）如图，在直角三角形ABC中，∠C=90°，AC=12．BC=16，点0为△ABC的内心，点M为斜边AB的中点，则OM的长为
（2011•德阳）如图，已知一次函数y=-x+1与反比例函数