ĢāÄæÄŚČŻ
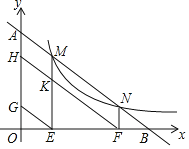
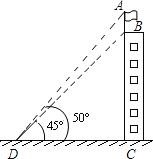
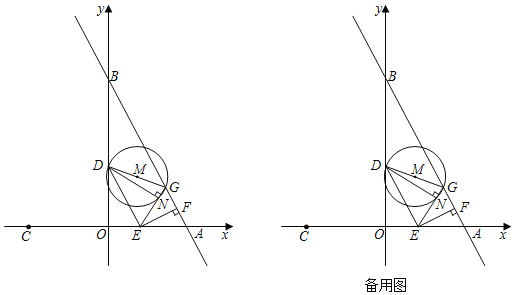
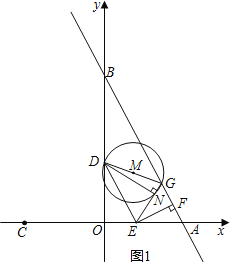
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy£½©2x+6ÓėxÖį£¬yÖį·Ö±š½»A£¬BĮ½µć£¬µćA¹ŲÓŚŌµćOµÄ¶Ō³ĘµćŹĒµćC£¬¶ÆµćE“ÓA³ö·¢ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½µćC£¬µćDŌŚĻ߶ĪOBÉĻĀś×ćtan”ĻDEO£½2£¬¹żEµć×÷EF”ĶABÓŚµćF£¬µćA¹ŲÓŚµćFµÄ¶Ō³ĘµćĪŖµćG£¬ŅŌDGĪŖÖ±¾¶×÷”ŃM£¬ÉčµćEŌĖ¶ÆµÄŹ±¼äĪŖtĆė£»
£Ø1£©µ±µćEŌŚĻ߶ĪOAÉĻŌĖ¶Æ£¬t£½””””Ź±£¬”÷AEFÓė”÷EDOµÄĻąĖʱČĪŖ1£ŗ![]() £»
£»
£Ø2£©µ±”ŃMÓėyÖįĻąĒŠŹ±£¬ĒótµÄÖµ£»
£Ø3£©ČōÖ±ĻßEGÓė”ŃM½»ÓŚµćN£¬ŹĒ·ń“ęŌŚtŹ¹NG£½![]() £¬Čō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
£¬Čō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©t£½
£»£Ø2£©t£½![]() »ņ5£»£Ø3£©“ęŌŚ£¬t£½
»ņ5£»£Ø3£©“ęŌŚ£¬t£½![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
£Ø1£©ĻČĒóÖ±ĻßÓė×ų±źÖįµÄ½»µć×ų±ź£¬ŌŁÖ¤”÷AEF”×”÷EDO”×”÷ABO£¬ÓÉ”÷AEFÓė”÷EDOµÄĻąĖʱČĪŖ1£ŗ![]() £¬¼“æÉĒóµĆtµÄÖµ£»
£¬¼“æÉĒóµĆtµÄÖµ£»
£Ø2£©ÓÉ”ŃMÓėyÖįĻąĒŠæÉÖŖ£ŗDG”ĶyÖį£¬·ÖĮ½ÖÖĒéæö£ŗ0”Üt”Ü3»ņ3£¼t”Ü6£¬·Ö±šÓÉD”¢GµÄׯ×ų±źĻąµČ½ØĮ¢·½³ĢĒó½ā¼“æÉ£»
£Ø3£©·ÖČżÖÖĒéæö£ŗ0”Üt”Ü![]() »ņ
»ņ![]() £¼t”Ü3»ņ3£¼t”Ü6£¬·Ö±š½ØĮ¢·½³ĢĒó½ā¼“æÉ£®
£¼t”Ü3»ņ3£¼t”Ü6£¬·Ö±š½ØĮ¢·½³ĢĒó½ā¼“æÉ£®
½ā£ŗ£Ø1£©ŌŚy£½©2x+6ÖŠ£¬Įīx£½0£¬µĆ£ŗy£½6£¬
Įīy£½0£¬µĆ£ŗ©2x+6£½0£¬
½āµĆ£ŗx£½3£¬
”ąA£Ø3£¬0£©£¬B£Ø0£¬6£©£¬C£Ø©3£¬0£©
”ąOA£½3£¬OB£½6£¬AB£½3![]() £¬AE£½t£¬OE£½3©t£¬
£¬AE£½t£¬OE£½3©t£¬
”ątan”ĻBAO£½![]() £½2
£½2
”ßtan”ĻDEO£½2
”ą”ĻBAO£½”ĻDEO
”ßEF”ĶAB
”ą”ĻAFE£½”ĻDOE£½90”ć
”ą”÷AEF”×”÷EDO”×”÷ABO
![]() £¬¼“
£¬¼“![]()
”ąAF£½![]() t£»
t£»
”ß”÷AEFÓė”÷EDOµÄĻąĖʱČĪŖ1£ŗ![]() £¬
£¬
”ą![]() £¬¼“OE£½
£¬¼“OE£½![]() AF
AF
”ą3©t£½![]() ”Į
”Į![]() t£¬
t£¬
½āµĆ£ŗt£½![]() £»
£»
¹Ź“š°øĪŖ£ŗt£½![]() £»
£»
£Ø2£©”ß”ŃMÓėyÖįĻąĒŠ
”ąDG”ĶyÖį
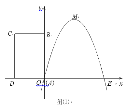
µ±0”Üt”Ü3Ź±£¬![]()
”ßtan”ĻDEO£½2
”ą![]()
”ą![]()
”ß![]() £¬”÷AEF”×”÷ABO
£¬”÷AEF”×”÷ABO
”ą![]()
”ą![]()
”ßµćA”¢G¹ŲÓŚµćF¶Ō³Ę
”ą![]()
”ą![]()
½«![]() “śČė
“śČė![]() ÖŠ£¬µĆ£¬
ÖŠ£¬µĆ£¬![]()
½āµĆ![]() £¬
£¬
”ąG£Ø3©![]() t£¬
t£¬![]() t£©£¬D£Ø0£¬6©2t£©£¬
t£©£¬D£Ø0£¬6©2t£©£¬
”ą![]() t£½6©2t£¬½āµĆ£ŗt£½
t£½6©2t£¬½āµĆ£ŗt£½![]() £»
£»
µ±3£¼t”Ü6Ź±£¬Ķ¬ĄķµĆG£Ø3©![]() t£¬
t£¬![]() t£©£¬D£Ø0£¬2t©6£©£¬
t£©£¬D£Ø0£¬2t©6£©£¬
”ą![]() t£½2t©6£¬½āµĆ£ŗt£½5£¬
t£½2t©6£¬½āµĆ£ŗt£½5£¬
×ŪÉĻĖłŹö£¬µ±”ŃMÓėyÖįĻąĒŠŹ±£¬t£½![]() »ņ5£»
»ņ5£»
£Ø3£©“ęŌŚ£®
µ±0”Üt”Ü![]() Ź±£¬G£Ø3©
Ź±£¬G£Ø3©![]() t£¬
t£¬![]() t£©£¬D£Ø0£¬6©2t£©£¬
t£©£¬D£Ø0£¬6©2t£©£¬
”ßµćA¹ŲÓŚµćFµÄ¶Ō³ĘµćĪŖµćG£¬EF”ĶAB
”ąEG£½EA£½t
”ß”ĻOEG£½”ĻOAB+”ĻEGA£½2”ĻOAB£¬”ĻOED£½”ĻOAB
”ą”ĻGED£½”ĻOED£½”ĻOAB
”ßDGĪŖÖ±¾¶
”ą”ĻDNG£½”ĻDNE£½”ĻDOE£½90”ć£¬DE£½DE
”ą”÷DEN”Õ”÷DEO£ØAAS£©
”ąEN£½OE£½3©t£¬NG£½EN©EG£½3©t©t£½3©2t£¬
”ą3©2t£½![]() £¬
£¬
½āµĆ£ŗt£½![]() £¬
£¬
µ±![]() £¼t”Ü3Ź±£¬NG£½EG©EN£½t©£Ø3©t£©£½2t©3
£¼t”Ü3Ź±£¬NG£½EG©EN£½t©£Ø3©t£©£½2t©3
”ą2t©3£½![]() £¬
£¬
½āµĆ£ŗt£½![]() £»
£»
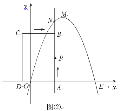
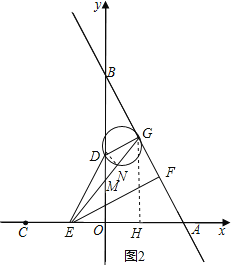
µ±3£¼t”Ü6Ź±£¬ČēĶ¼2£¬Į¬½ÓDN£¬¹żG×÷GH”ĶxÖįÓŚH£¬
”ßDGŹĒÖ±¾¶£¬
”ą”ĻDNG£½”ĻDNE£½90”ć£¬
”ß”ĻDMN£½”ĻEMO
”ą”÷DMN”×”÷EMO
”ą”ĻMDN£½”ĻOEM
”ßGH”ĪyÖį
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
ÓÉ£Ø2£©µĆ![]() £¬
£¬
”ß![]() Öį£¬
Öį£¬
”ą![]() £¬
£¬![]() £¬
£¬
”ą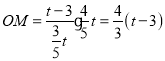 £¬
£¬
”ąDM£½OD©OM£½2£Øt©3£©©![]() £Øt©3£©£½
£Øt©3£©£½![]() £Øt©3£©
£Øt©3£©
”ßtan”ĻOEM£½![]()
”ąEM£½![]() OE£½
OE£½![]() £Øt©3£©£¬
£Øt©3£©£¬
”ąsin”ĻOEM£½![]() £½
£½![]() £½sin”ĻMDN£½
£½sin”ĻMDN£½![]()
”ąMN£½![]() ”Į
”Į![]() £Øt©3£©£½
£Øt©3£©£½![]() £Øt©3£©
£Øt©3£©
”ąNG£½EG©EM©MN£½t©![]() £Øt©3£©©
£Øt©3£©©![]() £Øt©3£©£½
£Øt©3£©£½![]() ©
©![]() t£¬
t£¬
”ą![]() £¬
£¬
½āµĆ£ŗt£½![]() £»
£»
×ŪÉĻĖłŹö£¬t£½![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø