题目内容
18.点A、B在数轴上的位置如图所示,点P是数轴上的一个动点,(1)当PB=2时,求点P表示的数?(2)当点P是线段AB的三等分点时,求点P表示的数?(3)当PB=2,且点M是线段AP的中点时,求线段AM的长度?(4)是否存在点P,使得PA+PB的值最小,若存在,确定点P在数轴上的位置,并求出PA+PB的最小值?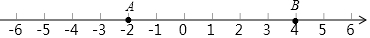
分析 (1)根据PB=2,分两种情况:①点P在点B的左边;②点P在点B的右边;分别求出点P表示的是什么数即可;
(2)根据点P是线段AB的三等分点,分两种情况:①AP=$\frac{1}{3}$AB;②BP=$\frac{1}{3}$AB;分别求出点P表示的是什么数即可;
(3)首先分两种情况,求出AP的长度是多少;然后根据点M是AP的中点,用线段AP的长度除以2,求出线段AM的长是多少即可;
(4)根据图示,可得当点P在A、B两点之间时,PA+PB的值最小,据此判断即可.
解答 解:(1)①点P在点B的左边时,
∵PB=2,4-2=2,
∴点P表示的是2.
②点P在点B的右边时,
∵PB=2,4+2=6,
∴点P表示的是6.
综上,可得点P表示的是2或6;
(2)∵4-(-2)=6,
∴线段AB的长度是6.
①AP=$\frac{1}{3}$AB=2时,点P表示的是-2+2=0.
②BP=$\frac{1}{3}$AB=2时,点P表示的是4-2=2.
综上,可得点P表示的是0或2;
(3)①点P在点B的左边时,
∵AP=6-2=4,4÷2=2,
∴线段AM的长是2.
②点P在点B的右边时,
∵AP=6+2=8,8÷2=4,
∴线段AM的长是4.
综上,可得
线段AM的长是2或4.
(4)根据图示,可得
当点P在A、B两点之间时,PA+PB的值最小,
此时,PA+PB=AB=6,
所以PA+PB的最小值是6.
点评 (1)此题主要考查了两点间的距离,要熟练掌握,解答此题的关键是要明确:连接两点间的线段的长度叫两点间的距离.(2)此题还考查了数轴的特征和应用,以及分类讨论思想的应用,要熟练掌握.

练习册系列答案
相关题目
6.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | xy-3=5 | C. | 3x-1=$\frac{x}{2}$ | D. | x+2y=1 |
10.下面是小玲同学在一次课堂测验中利用等式的性质解方程的过程,其中正确的是( )
| A. | -$\frac{1}{3}$x-5=4,得$\frac{1}{3}$x=4+5 | B. | 5y-3y+y=9,得(5-3)y=9 | ||
| C. | x+7=26,得x=19 | D. | -5x=20,得x=-$\frac{5}{20}$ |
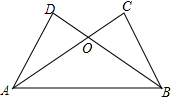 如图,已知AD=BC,AC=BD=10.
如图,已知AD=BC,AC=BD=10. 如图,阴影部分是一个正方形,则此正方形的面积为多少cm2?
如图,阴影部分是一个正方形,则此正方形的面积为多少cm2?