Question

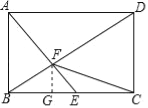
【题目】如图，在矩形中，，是的中点，于点，则的长是 ．

Answer 1

【答案】.

【解析】

试题分析：根据四边形ABCD是矩形，得到∠ABE=∠BAD=90°，根据余角的性质得到∠BAE=∠ADB，根据相似三角形的性质得到BE=1，求得BC=2，根据勾股定理得到AE=，BD=，根据三角形的面积公式得到BF=，过F作FG⊥BC于G，根据相似三角形的性质得到CG=，根据勾股定理即可得到结论．

∵四边形ABCD是矩形，∴∠ABE=∠BAD=90°，

∵AE⊥BD，∴∠AFB=90°，∴∠BAF+∠ABD=∠ABD+∠ADB=90°，

∴∠BAE=∠ADB，∴△ABE∽△ADB，∴，

∵E是BC的中点，∴AD=2BE，∴2BE2=AB2=2，∴BE=1，∴BC=2，

∴AE=，BD=，∴BF=，

过F作FG⊥BC于G，∴FG∥CD，∴△BFG∽△BDC，

∴，∴FG=，BG=，∴CG=，∴CF=．

故答案为．