题目内容
如图中，∠B=36°，∠C=76°，AD、AF分别是△ABC的角平分线和高，则∠DAF=________度．
20
分析：先根据三角形内角和定理及角平分线的性质求出∠BAD度数，再由三角形内角与外角的性质可求出∠ADF的度数，由AF⊥BC可求出∠AFD=90°，再由三角形的内角和定理即可解答．
解答：∵∠B=36°，∠C=76°，
∴∠BAC=180°-∠B-∠C=180°-36°-76°=68°，
∵AD是∠BAC的平分线，∴∠BAD=
×68°=34°，
∵∠ADC是△ABD的外角，∴∠ADC=∠B+∠BAD=36°+34°=70°，
∵AF⊥BC，
∴∠AFD=90°，
∴∠DAF=180°-∠ADC-∠AFD=180°-70°-90°=20°．
点评：本题涉及到三角形内角和定理、三角形外角的性质及角平分线的性质，难度中等．
分析：先根据三角形内角和定理及角平分线的性质求出∠BAD度数，再由三角形内角与外角的性质可求出∠ADF的度数，由AF⊥BC可求出∠AFD=90°，再由三角形的内角和定理即可解答．
解答：∵∠B=36°，∠C=76°，
∴∠BAC=180°-∠B-∠C=180°-36°-76°=68°，
∵AD是∠BAC的平分线，∴∠BAD=
×68°=34°，∵∠ADC是△ABD的外角，∴∠ADC=∠B+∠BAD=36°+34°=70°，
∵AF⊥BC，
∴∠AFD=90°，
∴∠DAF=180°-∠ADC-∠AFD=180°-70°-90°=20°．
点评：本题涉及到三角形内角和定理、三角形外角的性质及角平分线的性质，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
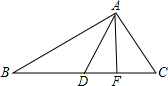如图中，∠B=36°，∠C=76°，AD、AF分别是△ABC的角平分线和高，则∠DAF=
15、在如图中，存在AB1，AB2，…AB8，AB9共九条线段，且点B1，B2，B3，…B9在同一条直线上，则图中三角形的个数是
