题目内容
抛物线y=3x2,y=-3x2,y=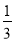 x2+3共有的性质是
x2+3共有的性质是
A.开口向上 B.对称轴是y轴
C.都有最高点 D.y随x值的增大而增大
B
【解析】三个图象的顶点的横坐标都是0,所以对称轴都是y轴.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
抛物线y=3x2,y=-3x2,y=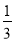 x2+3共有的性质是
x2+3共有的性质是
A.开口向上 B.对称轴是y轴
C.都有最高点 D.y随x值的增大而增大
B
【解析】三个图象的顶点的横坐标都是0,所以对称轴都是y轴.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案