题目内容
（2013•梧州模拟）一个边长为4的等边三角形ABC的高与⊙O的直径相等，如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E，则CE的长是（ ）分析：连接OC，并过点O作OF⊥CE于F，求出等边三角形的高即可得出圆的直径，继而得出OC的长度，在Rt△OFC中，可得出FC的长，利用垂径定理即可得出CE的长．
解答：解：连接OC，并过点O作OF⊥CE于F，
∵△ABC为等边三角形，边长为4，
∴△ABC的高为2
，
∴OC=
，
又∵∠ACB=60°，
∴∠OCF=30°，
在Rt△OFC中，可得FC=
，
即CE=2FC=3．
故选D．
∵△ABC为等边三角形，边长为4，
∴△ABC的高为2
| 3 |
∴OC=
| 3 |
又∵∠ACB=60°，
∴∠OCF=30°，
在Rt△OFC中，可得FC=
| 3 |
| 2 |
即CE=2FC=3．
故选D．
点评：本题主要考查了切线的性质和等边三角形的性质和解直角三角形的有关知识，题目不是太难，属于基础性题目．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
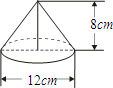（2013•梧州模拟）如图，一个圆锥形零件，高为8cm，底面圆的直径为12cm，则此圆锥的侧面积是（ ）
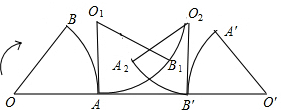（2013•梧州模拟）如图，已知扇形的圆心角为60°，半径为1，将它沿着箭头方向无滑动滚动到O′A′B′位置，则有：