题目内容
已知方程组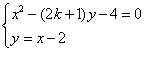
(1)求征:不论k为何值时,此方程组一定有实数解;
(2)设等腰△ABC的三边分别为a、b、c,其中c=4,且 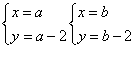 是该方程组的两个解,求△ABC的周长。
是该方程组的两个解,求△ABC的周长。
答案:
解析:
提示:
解析:
| 解:(1)把②代入①,并整理得x2-(2k+1)x+4k-2=0
∵△=[-(2k+1)]2-4(4k-2)=4k2-12k+9=(2k-3)2≥0 ∴方程组一定有实数根。 (2)∵x=a,x=b是方程x2-(2k+1)x+4k-2=0的两个实数根, ∴a+b=2k+1。 又∵△ABC是等腰三角形,∴a=b或a、b中有一个与c相等。 当a=b时,△=(2k-3)2=0, ∴k= 此时a+b=2k+1=4=c,不合题意,舍去。 当a≠b时,不妨设a=c=4。 代入③,得k= ∴a+b=2k+1=6>c。 ∴△ABC的周长a+b+c=10。
|
提示:
| 导析:判断方程组实数解的问题,首先要转化成一元二次方程实数根的判断,然后用根的判别式判断实数根的情况,从而得到方程组实数解的情况
|

练习册系列答案
相关题目
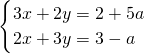

 ,1,3,4;
,1,3,4;