Question

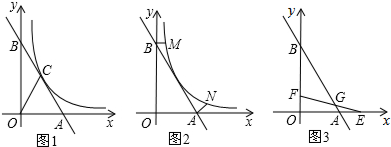
如图1，一次函数y=-2x+4的图象交x轴于点A，交y轴于点B，与反比例函数y=

k

x

(x＞0)的图象交于点C，连OC，若S_△AOC=2．
（1）求反比例函数的解析式；
（2）如图2，过点B作BM⊥OB交反比例函数y=

k

x

的图象于点M，点N为反比例函数y=

k

x

的图象上一点，∠ABM=∠BAN，求直线AN的解析式；
（3）如图3，点E在x轴上，点F在y轴上，OE=BF，EF交AB于点G，∠AGE=45°，求点G的坐标．

Answer 1

分析：（1）先由一次函数的解析式为y=-2x+4及x轴、y轴上点的坐标特征，求出A﹙2，0﹚，B﹙0，4﹚，再根据S_△AOC=2，利用三角形的面积公式求出C（1，2），然后运用待定系数法即可求出反比例函数的解析式；
（2）由A﹙2，0﹚，B﹙0，4﹚，C﹙1，2﹚三点的坐标，可知C为AB的中点，如图2，延长BM交AN的延长线于D，根据等角对等边得到DB=DA，再连结DC，由等腰三角形三线合一的性质得出DC⊥BA，则∠DCB=∠BOA=90°，由平行线的性质易得∠DBA=∠BAO，那么△DBC∽△BAO，得出DB：BC=BA：AO，求出DB=5，得到D﹙5，4﹚，然后运用待定系数法即可求出直线AN的解析式；
（3）设E（t，0），则F（0，4-t）．如图3，过点F作FH⊥AB于H，先解Rt△BFH，求出BH=

2 5

5

t，FH=

5

5

t=GH，则BG=

3 5

5

t，再设G（x，-2x+4），根据两点间的距离公式得出BG²=5x²=（

3 5

5

t）²，求出x=

3

5

t，则G（

3

5

t，-

6t

5

+4），然后根据E、G、F三点共线，列出方程

4-t-0

0-t

=

(4-t)-(- 6t 5 +4)

0- 3 5 t

，解方程求出t=3，进而得到G点坐标．

解答：解：（1）∵一次函数y=-2x+4的图象交x轴于点A，交y轴于点B，
∴A﹙2，0﹚，B﹙0，4﹚．
设C（m，n）．
∵S_△AOC=2，
∴

1

2

×2×n=2，
解得n=2．
又n=-2m+4，
∴m=1，
∴C（1，2），
所以反比例函数的解析式为y=

2

x

；

（2）∵A﹙2，0﹚，B﹙0，4﹚，C﹙1，2﹚，
∴C为AB的中点，AO=2，BO=4，AB=2

5

，
∴BC=

5

． 如图2，延长BM交AN的延长线于D，
∵∠ABM=∠BAN，
∴DB=DA，
连结DC，则DC⊥BA，
∵BM⊥OB，
∴BM∥OA，
∴∠DBA=∠BAO，
又∠DCB=∠BOA=90°，
∴△DBC∽△BAO，
∴DB：BC=BA：AO，即DB：

5

=2

5

：2，
∴DB=5，
∴D﹙5，4﹚．
设直线AN的解析式为y=mx+b，
∵直线AN过A﹙2，0﹚、D﹙5，4﹚，
∴

2m+b=0 5m+b=4

，

m= 4 3 b=- 8 3

∴直线AN的解析式为y=

4

3

x-

8

3

；

（3）设E（t，0），则F（0，4-t）．
如图3，过点F作FH⊥AB于H．
在Rt△BFH中，∵∠BHF=90°，BF=OE=t，
∴BH=BF•cos∠B=t•

4

2 5

=

2 5

5

t，FH=BF•sin∠B=t•

2

2 5

=

5

5

t，
∵∠AGE=45°=∠HGF，
∴HG=FH=

5

5

t，
∴BG=BH+HG=

2 5

5

t+

5

5

t=

3 5

5

t．
设G（x，-2x+4），
∵B﹙0，4﹚，
∴BG²=（x-0）²+（-2x+4-4）²=5x²，
∴5x²=（

3 5

5

t）²，
∴x=

3

5

t（负值舍去），
∴G（

3

5

t，-

6t

5

+4）．
∵E、G、F三点共线，
∴

4-t-0

0-t

=

(4-t)-(- 6t 5 +4)

0- 3 5 t

，
解得t=3，
∴G（

9

5

，

2

5

）．

点评：本题是反比例函数综合题，其中涉及到运用待定系数法求反比例函数、一次函数的解析式，三角形的面积，等腰三角形、相似三角形的判定与性质，坐标轴上点的坐标特征，中点坐标、两点间的距离公式，解直角三角形等知识，综合性较强，有一定难度．正确作出辅助线是解题的关键．