题目内容
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于点E,EF⊥AB于点F,若CE=1, ,求EF的长.
,求EF的长.
【答案】分析:Rt△ABE中,EF⊥AB,易得∠AEF=∠B,即cos∠B= ,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC-BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC-BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
解答: 解:∵AE⊥BC,∴∠AEF+∠1=90°;
解:∵AE⊥BC,∴∠AEF+∠1=90°;
∵EF⊥AB,∴∠1+∠B=90°;
∴∠B=∠AEF;(1分)
∴
∵在Rt△ABE中,∠AEB=90°
∴ ;(2分)
;(2分)
设BE=4k,AB=5k,∵BC=AB,∴EC=BC-BE=BA-BE=k;
∵EC=1,∴k=1;(3分)
∴BE=4,AB=5;
∴AE=3;(4分)
在Rt△AEF中,∠AFE=90°,
∵ ,(5分)
,(5分)
∴ .(6分)
.(6分)
点评:此题主要考查了直角三角形的性质、等腰三角形的性质、锐角三角函数的应用等知识.
 ,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC-BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC-BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.解答:
 解:∵AE⊥BC,∴∠AEF+∠1=90°;
解:∵AE⊥BC,∴∠AEF+∠1=90°;∵EF⊥AB,∴∠1+∠B=90°;
∴∠B=∠AEF;(1分)
∴

∵在Rt△ABE中,∠AEB=90°
∴
 ;(2分)
;(2分)设BE=4k,AB=5k,∵BC=AB,∴EC=BC-BE=BA-BE=k;
∵EC=1,∴k=1;(3分)
∴BE=4,AB=5;
∴AE=3;(4分)
在Rt△AEF中,∠AFE=90°,
∵
 ,(5分)
,(5分)∴
 .(6分)
.(6分)点评:此题主要考查了直角三角形的性质、等腰三角形的性质、锐角三角函数的应用等知识.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
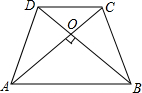 已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13
已知:如图,等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于O,BC=13 8、已知:如图,等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D,E.
8、已知:如图,等腰直角三角形ABC中,∠ACB=90°,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D,E. 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. 7、已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:BE2=EF•EG.
7、已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:BE2=EF•EG. 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,cos∠AEF=
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,cos∠AEF=