题目内容
如图1,△ABC中,AB=AC,∠BAC=130°,边AB、AC的垂直平分线交BC于点P、Q.

(1)求∠PAQ的度数;
(2)如图2,△ABC中,AB>AC,且90°<∠BAC<180°,边AB、AC的垂直平分线交BC于点P、Q.
①若∠BAC=130°,则∠PAQ=______°,若∠BAC=α,则∠PAQ用含有α的代数式表示为______;
②当∠BAC=______°时,能使得PA⊥AQ;
③若BC=10cm,则△PAQ的周长为______cm.
解:(1)∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=130°,
∴∠B+∠C=180°-∠BAC=50°,
∴∠BAP+∠CAQ=50°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°;
(2)①∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=130°,
∴∠B+∠C=180°-∠BAC=50°,
∴∠BAP+∠CAQ=50°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°;
∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=α,
∴∠B+∠C=180°-∠BAC=180°-α,
∴∠BAP+∠CAQ=180°-α,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=α-(180°-α)=2α-180°;
②当∠PAQ=90°,
即2α-180°=90°时,PA⊥AQ,
解得:α=135°,
∴当∠BAC=135°时,能使得PA⊥AQ;
③∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∵BC=10cm,
即BP+PQ+CQ=AP+PQ+AQ=10cm,
∴△PAQ的周长为10cm.
故答案为:①80,2α-180°;②135;③10.
分析:(1)由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后根据等边对等角的性质,求得∠BAP=∠B,∠CAQ=∠C,又由三角形内角和定理,即可求得∠BAP+∠CAQ的度数,继而求得∠PAQ的度数;
(2)①由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后根据等边对等角的性质,求得∠BAP=∠B,∠CAQ=∠C,又由三角形内角和定理,即可求得∠BAP+∠CAQ的度数,继而求得∠PAQ的度数;
②根据①中的结论,可得方程2α-180°=90°,继而求得∠BAC的度数;
③由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后利用等量代换的知识,即可求得△PAQ的周长.
点评:此题考查了线段垂直平分线的性质、三角形内角和定理、垂直的定义以及等腰三角形的性质.此题综合性较强,难度适中,解题的关键是注意数形结合思想与整体思想的应用,注意等量代换知识的应用.
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=130°,
∴∠B+∠C=180°-∠BAC=50°,
∴∠BAP+∠CAQ=50°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°;
(2)①∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=130°,
∴∠B+∠C=180°-∠BAC=50°,
∴∠BAP+∠CAQ=50°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°;
∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∵∠BAC=α,
∴∠B+∠C=180°-∠BAC=180°-α,
∴∠BAP+∠CAQ=180°-α,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=α-(180°-α)=2α-180°;
②当∠PAQ=90°,
即2α-180°=90°时,PA⊥AQ,
解得:α=135°,
∴当∠BAC=135°时,能使得PA⊥AQ;
③∵边AB、AC的垂直平分线交BC于点P、Q,
∴AP=BP,AQ=CQ,
∵BC=10cm,
即BP+PQ+CQ=AP+PQ+AQ=10cm,
∴△PAQ的周长为10cm.
故答案为:①80,2α-180°;②135;③10.
分析:(1)由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后根据等边对等角的性质,求得∠BAP=∠B,∠CAQ=∠C,又由三角形内角和定理,即可求得∠BAP+∠CAQ的度数,继而求得∠PAQ的度数;
(2)①由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后根据等边对等角的性质,求得∠BAP=∠B,∠CAQ=∠C,又由三角形内角和定理,即可求得∠BAP+∠CAQ的度数,继而求得∠PAQ的度数;
②根据①中的结论,可得方程2α-180°=90°,继而求得∠BAC的度数;
③由边AB、AC的垂直平分线交BC于点P、Q,根据线段垂直平分线的性质,即可得AP=BP,AQ=CQ,然后利用等量代换的知识,即可求得△PAQ的周长.
点评:此题考查了线段垂直平分线的性质、三角形内角和定理、垂直的定义以及等腰三角形的性质.此题综合性较强,难度适中,解题的关键是注意数形结合思想与整体思想的应用,注意等量代换知识的应用.

练习册系列答案
相关题目
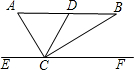 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )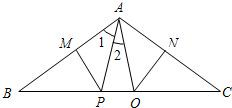 如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.
如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数. 19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.
19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.