题目内容
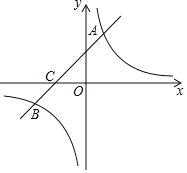
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
【答案】⑴![]() ,
,![]() ;⑵
;⑵![]() 的最大值为
的最大值为![]() ,
,![]() ;⑶
;⑶![]() 或
或![]() .
.
【解析】
(1)利用待定系数法,即可得到反比例函数和一次函数的解析式;
(2)根据一次函数y1=x+2,求得与y轴的交点P,此交点即为所求;
(3)根据AB两点的横坐标及直线与双曲线的位置关系求x的取值范围.
⑴.∵![]() 在反比例函数
在反比例函数![]() 上
上
∴![]()
∴反比例函数的解析式为![]()
把![]() 代入
代入![]() 可求得
可求得![]()
∴![]() .
.
把![]() 代入
代入![]() 为
为![]() 解得
解得![]() .
.
∴一次函数的解析式为![]() .
.
⑵![]() 的最大值就是直线
的最大值就是直线![]() 与两坐标轴交点间的距离.
与两坐标轴交点间的距离.
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
令![]() ,则
,则![]() ,解得
,解得![]() ,∴
,∴![]()
令![]() ,则
,则![]() ,,∴
,,∴![]()
∴![]() ,
,![]()
∴![]() 的最大值为
的最大值为![]() .
.
⑶根据图象的位置和图象交点的坐标可知:
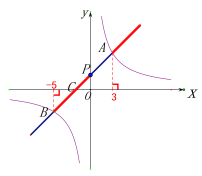
当![]() 时
时![]() 的取值范围为;
的取值范围为;![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.

【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成不完整的统计表与统计图,请结合图中的信息解答下列问题.
学生最喜欢的图书类别人数统计表
图书类别 | 画记 | 人数 | 百分比 |
文学类 | |||
艺体类 | 正 | 5 | |
科普类 | 正正一 | 11 | 22% |
其它 | 正正 | 14 | 28% |
合计 | a | 100% |


(1)随机抽取的样本容量a为_________________________;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生人数.