题目内容
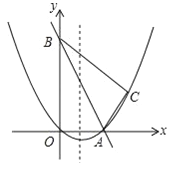
【题目】△ABC内接于O，AB＝AC，D在劣弧AC上，∠ABD＝45°
(1) 如图1，BD交AC于E，连CD．若AB＝BD，求证：CD＝
DE
(2) 如图2，连AD、CD，已知sin∠BDC＝
，求tan∠CBD的值
【答案】(1) CD＝
DE(2) tan∠CBD＝
【解析】(1) ∵AC＝BD
∴弧AC＝弧BD
∴弧BC＝弧AD
∴∠BAC＝∠ABD＝∠BDC
又∠ACD＝∠ABD＝45°
∴△CDE为等腰直角三角形
∴CD＝
DE
(2) 延长AO交BC于F，连结OC、OD、OB
∵∠BAC＝∠BDC，∠BAC＝
∠BOC
又∠COF＝
∠BOC
∴COF＝BDC
∵sin∠BDC＝sin∠COF＝
设FC＝12，OC＝13，则OF＝5
∵∠ABD＝45°
∴∠AOD＝90°
设AF与BD交于点G
∴△BFG∽△DOG
∴
，
∴tan∠CBD＝
练习册系列答案
阅读快车系列答案
相关题目
