��Ŀ����
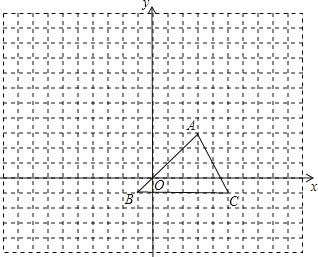
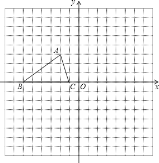
����Ŀ����ͼ��������y��ax2+bx+3��x���ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
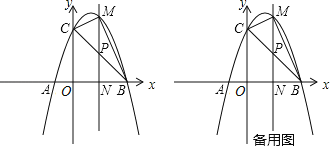
��2������BC������PΪ�߶�BC�ϵ�һ�����㣨�����B����C�غϣ�������P��ֱ��PN��x���ڵ�N�����������ڵ�M������BCM������ʱ�����BPN���ܳ���
��3���ڣ�2���������£�����BCM������ʱ���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��CNQΪ���������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+2x+3 ��2��![]() ��3��������
��3��������
��������
��1����A��B��������뵽����ʽ����⼴�ɣ�
��2�����ֱ��BC�Ľ���ʽ��Ȼ�������BCM�ı���ʽ����һ�����κ����������ȡ���ֵ��������Ȼ�����ù��ɶ��������BPN���ܳ���
��3��C��N������֪���Q����Ϊ��1��a������������֮��ľ��빫ʽ��ʾ��CQ��QN��CNȻ��������������CQ��QN����CQ��CN����QN��CN������ʽ���.
�⣺��1������A����1��0����B��3��0������������ʽ�еã�![]() �����
�����![]() ��
��
�������߽���ʽΪy����x2+2x+3��
��2����ֱ��BC�Ľ���ʽΪ��y��kx+b��
���У�![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y����x+3��
��P��x����x+3������M��x����x2+2x+3����
��PM������x2+2x+3��������x+3������x2+3x��
��![]()
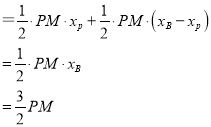 ��
��
��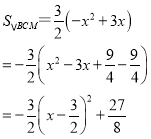
�൱![]() ʱ����BCM��������
ʱ����BCM��������
��ʱ![]() ��
��
��PN��ON��![]() ��
��
��![]() ��
��
��Rt��BPN�У��ɹ��ɶ����ã�![]() ��
��
![]() ��
��
�൱��BCM��������ʱ����BPN���ܳ�Ϊ![]() ��
��
��3���ɣ�2��֪P������Ϊ![]() ����
����![]() ��
��
��y����x2+2x+3������x��1��2+4��
�������ߵĶԳ���Ϊx��1��
��Q��1��a������C��0��3����![]() ��
��
��![]() ��
��![]() ������֮����빫ʽ����
������֮����빫ʽ����
����CNQΪ���������Σ��ɷ����������
�ٵ�CQ��QNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ![]() ��
��
�ڵ�CQ��CNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ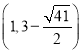 ��
��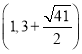 ��
��
�۵�QN��CNʱ��![]() ����ã�
����ã�![]() ��
��
���Q������Ϊ![]() ��
��![]() ��
��
�ۺ����Ͽɵõ�Q������Ϊ![]() ��
��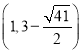 ��
��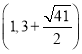 ��
��![]() ��
��![]() ��
��

 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�