题目内容
已知:P为半径为5的⊙O内一点,过P点最短的弦长为8,则OP的长 .
【答案】分析:由题意可知,过P点最短的弦长为8,此弦和过点P的半径垂直,根据垂径定理和勾股定理求解即可.
解答:解:连接OP,作OP⊥AB与P,则OP为所求,
∴AP=BP= AB=4,
AB=4,
∵OB=5,
∴在直角△OBP中,根据勾股定理得到:OP= =3,
=3,
故答案为:3.
点评:此题考查圆中求弦心距的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.
解答:解:连接OP,作OP⊥AB与P,则OP为所求,

∴AP=BP=
 AB=4,
AB=4,∵OB=5,
∴在直角△OBP中,根据勾股定理得到:OP=
 =3,
=3,故答案为:3.
点评:此题考查圆中求弦心距的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
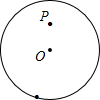 能用一句话归纳你的发现吗?
能用一句话归纳你的发现吗?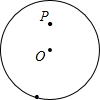 能用一句话归纳你的发现吗?
能用一句话归纳你的发现吗? ,求PC、PD的长.
,求PC、PD的长.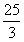 ,求PC、PD的长。
,求PC、PD的长。 