题目内容
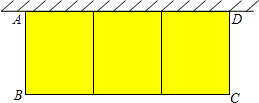如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，墙的最大可用长度为8米，设花圃的宽AB为x米，面积为S平方米．（1）求S与x的函数关系式；
（2）求自变量的取值范围；
（3）当x取何值时所围成的花圃面积最大，最大值是多少？
分析：（1）求出S=AB×BC代入即可；
（2）利用0＜24-4x≤8进而解出即可；
（3）把解析式化成顶点式，再利用二次函数增减性即可得到答案．
（2）利用0＜24-4x≤8进而解出即可；
（3）把解析式化成顶点式，再利用二次函数增减性即可得到答案．
解答：解：（1）设花圃的宽AB为x米，则BC=（24-4x）m，
根据题意得出：S=x（24-4x）=-4x2+24x；
（2）∵墙的可用长度为8米
∴0＜24-4x≤8
解得：4≤x＜6；
（3）S=-4x2+24x=-4（x2-6x）=-4（x-3）2+36，
∵4≤x＜6，
∴当x=4m时，S最大值=32 平方米．
根据题意得出：S=x（24-4x）=-4x2+24x；
（2）∵墙的可用长度为8米
∴0＜24-4x≤8
解得：4≤x＜6；
（3）S=-4x2+24x=-4（x2-6x）=-4（x-3）2+36，
∵4≤x＜6，
∴当x=4m时，S最大值=32 平方米．
点评：本题主要考查对二次函数的最值，二次函数的解析式，解一元二次方程等知识点的理解和掌握，能把实际问题转化成数学问题是解此题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
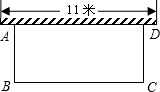边不超过墙长），设与墙平行的一边BC的长为x米，面积为y平方米．
与墙平行的一边BC的长为x米，面积为y平方米．
与墙平行的一边BC的长为x米，面积为y平方米．
