题目内容
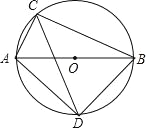
【题目】已知两条线段AC和BC,连接AB,分别以AB、BC为底边向上画等腰△ABD和等腰△BCE,∠ADB=∠BEC=α.
(1)如图1,当α=60°时,求证:△DBE≌△ABC;
(2)如图2,当α=90°时,且BC=5,AC=2.
①求DE的长;
②如图3,将线段CA绕点C旋转,点D也随之运动,请求出C,D两点之间距离的取值范围.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)只要证明△DBA,△EBC都是等边三角形即可解决问题;
(2)①只要证明△DBE∽△ABC,推出![]() ,即可解决问题;
,即可解决问题;
②在△DEC中,根据三边关系即可解决问题.
(1)如图1.

∵DB=DA,EB=EC,∠BDA=∠BEC=60°,∴△ABD,△EBC都是等边三角形,∴BD=BA,BE=BC,∠DBA=∠EBC=60°,∴∠DBE=∠ABC,∴△DBE≌△ABC.
(2)①∵△ABD,△BEC都是等腰直角三角形,∴![]() ,∠DBA=∠EBC=45°,∴∠DBE=∠ABC,∴△DBE∽△ABC,∴
,∠DBA=∠EBC=45°,∴∠DBE=∠ABC,∴△DBE∽△ABC,∴![]() .
.
∵AC=2,∴DE![]() .
.

②如图3中,连接CD.

由(2)可知DE![]() .在Rt△BCE中,EC
.在Rt△BCE中,EC![]() BC
BC![]() .
.
∵EC﹣DE≤DC≤EC+DE,∴![]() DE
DE![]() .
.

练习册系列答案
相关题目
【题目】如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形,……
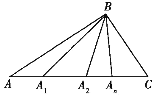
(1)完成下表:
连接个数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现三角形个数 | 3 | 6 |
(2)若出现了45个三角形,则共连接了_____个点?若一直连接到An,则图中共有______个三角形.