题目内容
已知△ABC.
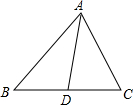
(1)如图,AC⊥AB,点D为BC上一点,∠ABD=∠BAD,∠EAC=∠CAD,
求证:AE∥BC.
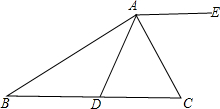
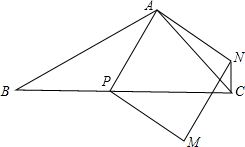
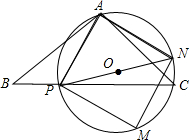
(2)如图,点P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,则∠ACB=______°,并证明你的结论.
 解:(1)证明:∵AC⊥AB,
解:(1)证明:∵AC⊥AB,∴∠ABC+∠ACB=90°,∠BAD+∠DAC=90°;
∵已知∠ABD=∠BAD,
∴∠ACB=∠DAC,
又∵已知∠EAC=∠CAD,
∴∠EAC=∠ACB,
∴AE∥BC.
(2)∠ACB=45°;
证明:连接PN,并经PN为直径作圆O,则正方形APMN为圆O的内接正方形;
∵NC⊥BC,∴点C在圆上,
∵PN为正方形的对角线,
∴∠ANP=45°,
∴∠ACB=45°(同弧对应的圆周角相等).
分析:(1)由AC⊥AB,可得∠ABC+∠ACB=90°,∠BAD+∠DAC=90°;由∠ABD=∠BAD,可得:∠ACB=∠DAC,又因为∠EAC=∠CAD,所以可得∠EAC=∠ACB,即可证明AE∥BC.
(2)连接PN,并以PN为直径作圆O,则正方形APMN为圆O的内接正方形;由NC⊥BC可得点C在圆上,据正方形的性质可得∠ANP=45°,由同弧对应的圆周角相等可知∠ACB=45°.
点评:本题考查了平行线的判定,正方形的性质及圆的性质,是一道考查学生综合能力的好题,正确作出辅助线是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
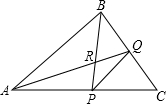 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于