Question

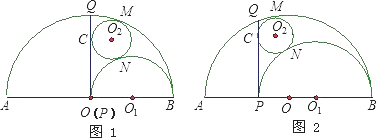
已知AB是半圆O的直径，AB=16，P点是AB上的一动点（不与A、B重合），PQ⊥AB，垂足为P，交半圆O于Q；PB是半圆O₁的直径，⊙O₂与半圆O、半圆O₁及PQ都相切，切点分别为M、N、C．
（1）当P点与O点重合时（如图1），求⊙O₂的半径r；
（2）当P点在AB上移动时（如图2），设PQ=x，⊙O₂的半径r．求r与x的函数关系式，并求出r取值范围．

Answer 1

分析：（1）、由勾股定理得OO₂²-OD²=O₂D²=O₁O₂²-O₁D²，可求得r的值；
（2）、连接O₁O₂、OO₂，作O₂D⊥AB于D，由射影定理和勾股定理可求得r与x的函数关系式．

解答：解：（1）连接OO₂、O₁O₂、O₂C，作O₂D⊥AB于D．（1分）
∵⊙O₂与⊙O、⊙O₁、PQ相切，
∴OO₂=8-r，（2分）
O₁O₂=4+r．（3分）
∵四边形ODO₂C是矩形，
∴OD=r，O₁D=4-r（4分）
根据勾股定理得：OO₂²-OD²=O₂D²=O₁O₂²-O₁D²，
即：（8-r）²-r²=（r+4）²-（4-r）²，（5分）
∴r=2；（6分）

（2）∵AB是⊙O直径，PQ⊥AB
∴PQ²=AP•PB
设⊙O₁半径是a，
则x²=2a（16-2a）=4（8a-a²）．
连接O₁O₂、OO₂，作O₂D⊥AB于D
∴O₁O₂=a+r，OO₂=8-r，O₁D=O₁P-PD=a-r，OD=PB-PD-OB=2a-r-8，（8分）
根据勾股定理得；O₁O₂²-O₁D²=OO₂²-OD²，
即：（a+r）²-（a-r）²=（8-r）²-（2a-r-8）²，（9分）
化简得：8r=8a-a²．
∴x²=32r，即r=

1

32

x2（10分）
∵0≤x≤8，
∴0＜r≤2．（12分）
说明：其它解法相应给分

点评：圆与圆相切，一般通过构造直角三角形，矩形，利用勾股定理和矩形的性质，圆心距与圆的半径求解．