题目内容
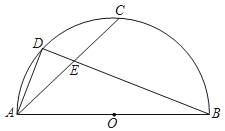
【题目】如图,AB为⊙O的直径,C为⊙O上一点,点D为半圆AB的中点,CD交AB于点E,若AC=8,BC=6,则BE的长为( )

A.4.25B.![]() C.3
C.3![]() D.4.8
D.4.8
【答案】B
【解析】
连接OD,作CH⊥AB于H,先利用勾股定理算出AB的长度,再根据等面积法算出CH,进而算出BH,利用△CHE∽△DOE对应边成比例求出OE与EH的关系式,通过列式算出EH即可算出BE.
连接OD,作CH⊥AB于H,如图,

∵AB为⊙O的直径,
∴∠ACB=90°,
∴AB=![]() =10,
=10,
∵![]() CHAB=
CHAB=![]() ACBC,
ACBC,
∴CH=![]() =
=![]() ,
,
在Rt△BCH中,BH= =
=![]() ,
,
∵点D为半圆AB的中点,
∴OD⊥AB,
∴OD∥CH,
∴△CHE∽△DOE,
∴EH:OE=CH:OD=![]() :5=24:25,
:5=24:25,
∴OE=![]() EH,
EH,
∵![]() EH+EH+
EH+EH+![]() =5,
=5,
∴EH=![]() ,
,
∴BE=EH+BH=![]() +
+![]() =
=![]() .
.
故选:B.

 同步练习强化拓展系列答案
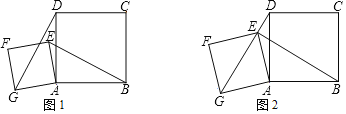
同步练习强化拓展系列答案【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,点E是线段AD上的一个动点,连接EC,线段EC绕点E顺时针旋转60°得到线段EF,连接DF、BF,已知AD=5cm,BC=8cm,设AE=xcm,DF=y1cm,BF=y2cm.小王根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小王的探究过程,请补充完整:
(1)对照下表中自变量x的值进行取点,画图,测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.52 | 2.07 | 2.05 | 2.48 |
| 4.00 |
y2/cm | 1.93 | 2.93 | 3.93 | 4.93 | 5.93 | 6.93 |
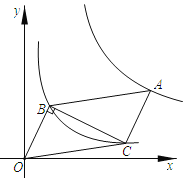
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象:

(3)结合函数图象,解决问题:
①当AE的长度约为_______cm时,DF最小;
②当△BDF是以BF为腰的等腰三角形时,AE的长度约为______cm.