题目内容
已知:对于实数a,只有一个实数值x满足等式
+
+
=0,试求所有这样的实数a的和.
| x+1 |
| x-1 |
| x-1 |
| x+1 |
| 2x+a+2 |
| x2-1 |
方程两边都乘以(x+1)(x-1)得,(x+1)2+(x-1)2+2x+a+2=0,
整理得,2x2+2x+a+4=0,①
△=b2-4ac=22-4×2×(a+4)=-8a-28,
(1)当方程①有两个相等的实数根时,△=0,
即-8a-28=0,
解得a1=-
,
此时方程①有一个根x=-
,验证可知x=-
的确满足题中的等式,
(2)当方程①有两个不相等的实数根时,△>0,
即-8a-28>0,
解得a<-
,
(i)若x=1是方程①的根,则原方程有增根x=1,代入①得,2+2+a+4=0,
解得a2=-8,
此时方程①的另一个根x=-2,它的确也满足题中的等式;
(ii)若x=-1是方程①的根,则原方程有增根x=-1,代入①得,2-2+a+4=0,
解得a3=-4,
此时方程①的另一个根x=0,验证可知x=0的确满足题中的等式;
因此a1=-
,a2=-8,a3=-4即为所求,
a1+a2+a3=-
-8-4=-
.
故答案为:-
.
整理得,2x2+2x+a+4=0,①
△=b2-4ac=22-4×2×(a+4)=-8a-28,
(1)当方程①有两个相等的实数根时,△=0,
即-8a-28=0,
解得a1=-
| 7 |
| 2 |
此时方程①有一个根x=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)当方程①有两个不相等的实数根时,△>0,
即-8a-28>0,
解得a<-
| 7 |
| 2 |
(i)若x=1是方程①的根,则原方程有增根x=1,代入①得,2+2+a+4=0,
解得a2=-8,
此时方程①的另一个根x=-2,它的确也满足题中的等式;
(ii)若x=-1是方程①的根,则原方程有增根x=-1,代入①得,2-2+a+4=0,
解得a3=-4,
此时方程①的另一个根x=0,验证可知x=0的确满足题中的等式;
因此a1=-
| 7 |
| 2 |
a1+a2+a3=-
| 7 |
| 2 |
| 31 |
| 2 |
故答案为:-
| 31 |
| 2 |

练习册系列答案
相关题目
 ≥0,∴a-
≥0,∴a-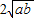 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2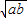 ,只有点a=b时,等号成立.
,只有点a=b时,等号成立.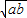 (a,b均为正实数)中,若ab为定值p,则a+b≥
(a,b均为正实数)中,若ab为定值p,则a+b≥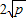 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2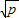 .
.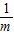 有最小值______;
有最小值______;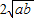 ,并指出等号成立时的条件;
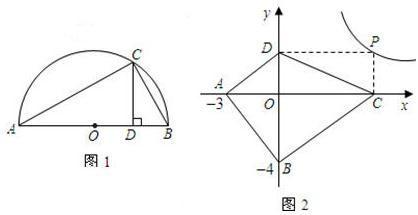
,并指出等号成立时的条件;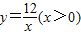 上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.