题目内容
(本题满分10分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)求证:BC 2=BDBA;(2)判断DE与⊙O位置关系,并说明理由.
(1)见解析;(2)相切.
【解析】
试题分析:(1)根据直径可得∠ADC=∠BDC=90° 根据∠ACB=90° ∠B=∠B得出△BCD和△BAC相似,从而得出结论;(2)连接OD,根据直角三角形斜边上的中线的性质得出∠EDC=∠ECD,根据OD=OC得出∠ODC=∠OCD,根据∠OCD+∠DCE=90°得出∠EDC+∠ODC=90°,从而说明∠EDO=90°,得出相切.
试题解析:(1)∵AC为 的直径. ∴
的直径. ∴ ∴
∴
又∵ ∴
∴ 又∵
又∵
∴△BCD∽△BAC ∴ 即
即
(2)DE与 相切 连结DO
相切 连结DO

∵ ,E为BC的中点.
,E为BC的中点.
∴ ∴∠EDC=∠ECD
∴∠EDC=∠ECD
又∵在 中,OD=OC ∴
中,OD=OC ∴ 而
而
∴ 即
即 ∴
∴
又∵点D在 上 ∴DE与
上 ∴DE与 相切
相切
考点:三角形相似的应用,切线的判定.

练习册系列答案
相关题目
 的边长为1,∠
的边长为1,∠ =60°;作
=60°;作 ⊥
⊥ 于点
于点 ,以
,以 为一边,做第二个菱形
为一边,做第二个菱形 ,使∠
,使∠ =60°;作
=60°;作 ⊥
⊥ 于点
于点 ,以
,以 为一边做第三个菱形
为一边做第三个菱形
 =60°;
=60°; 依此类推,这样做的第
依此类推,这样做的第 个菱形
个菱形 的边
的边 的长是 .
的长是 .
 元 D.
元 D. 元
元 精确到 位,
精确到 位, 的算术平方根是 .
的算术平方根是 . =±4 B.
=±4 B. =-9 C.
=-9 C. =-3 D.
=-3 D.
 .
. ”“
”“ ”或 “
”或 “ ”).
”).

 <180°,其它条件不变,如图③,你认为(1)中的结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF、EF与DE之间的关系,并说明理由。
<180°,其它条件不变,如图③,你认为(1)中的结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF、EF与DE之间的关系,并说明理由。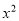 =80 (D)60
=80 (D)60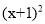 =80
=80