题目内容
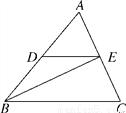
如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案