题目内容
如图①,平面直角坐标系中,点A、B在x轴上,点C在第一象限,AC=BC,点D、E分别是AC、BC的中点.已知A、D两点的坐标分别为(-3,0)、(0,4),
(1)直接写出下列各点的坐标:
B
(2)如图②动点P从点A出发,沿A→D→E的方向向点E运动(不与E重合),同时动点M从点D出发,沿D→E→B的方向向点B运动(不与B重合),P、M运动的速度均为每秒1个单位,过点P的直线l与线段BC平行,交线段AB于点Q,设运动时间为t秒(t>0),
①直接写出t的取值:
当
当
②求△BQM的面积S与运动时间t的函数关系式,并写出相应的t的取值范围.

(1)直接写出下列各点的坐标:
B
(9,0)
(9,0)
;C(3,8)
(3,8)
;E(6,4)
(6,4)
;(2)如图②动点P从点A出发,沿A→D→E的方向向点E运动(不与E重合),同时动点M从点D出发,沿D→E→B的方向向点B运动(不与B重合),P、M运动的速度均为每秒1个单位,过点P的直线l与线段BC平行,交线段AB于点Q,设运动时间为t秒(t>0),
①直接写出t的取值:
当
5≤t<11
5≤t<11
时,四边形PQBE为平行四边形;当
t=6
t=6
时,四边形PQBM为菱形;②求△BQM的面积S与运动时间t的函数关系式,并写出相应的t的取值范围.

分析:(1)设过点A、D的直线解析式为y=kx+b,把点A(-3,0)、D(0,4)代入即可求出直线AD的解析式,再由两点间的距离公式求出线段AD的长,设出C点坐标,由AD=CD即可得出C点坐标,过点C作CH⊥x轴于点H,由AC=BC可知点D与点E,点A与点B关于直线CH对称,故可得出B、E两点的坐标;
(2)①先求出AB的长,再根据D、E分别是AC、BC的中点可知DE是△ABC的中位线,故可求出DE的长,由于PQ∥BC,故可得出当点P、点M在线段DE上时四边形PQBE为平行四边形,再由AD+DE=5+6=11,P、M运动的速度均为每秒1个单位即可得出当四边形PQBE为平行四边形时t的取值范围;再由四边形PQBM为菱形,PQ∥BE,故M、E重合,由此即可得出t的值;
②由于当0<t<5时,点P在AD上,点M在DE上;当5≤t≤6时,点P、点M均在DE上;当6<t<11时,点P在DE上,点M在EB上故应分三种情况进行讨论.
(2)①先求出AB的长,再根据D、E分别是AC、BC的中点可知DE是△ABC的中位线,故可求出DE的长,由于PQ∥BC,故可得出当点P、点M在线段DE上时四边形PQBE为平行四边形,再由AD+DE=5+6=11,P、M运动的速度均为每秒1个单位即可得出当四边形PQBE为平行四边形时t的取值范围;再由四边形PQBM为菱形,PQ∥BE,故M、E重合,由此即可得出t的值;
②由于当0<t<5时,点P在AD上,点M在DE上;当5≤t≤6时,点P、点M均在DE上;当6<t<11时,点P在DE上,点M在EB上故应分三种情况进行讨论.
解答: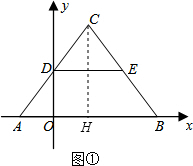 解:(1)设过点A、D的直线解析式为y=kx+b,
解:(1)设过点A、D的直线解析式为y=kx+b,
∵点A(-3,0)、D(0,4)代入得
,
解得
,
∴直线AD的解析式为y=
x+4,
∴AD=
=5,
∵点D、E分别是AC、BC的中点,
∴CD=AD=5,
设点C(x,
x+4),则
CD=
=
,
解得x1=3或x2=-3(舍去),
∴C(3,8),
如图①,过点C作CH⊥x轴于点H,则直线CH的解析式为x=3,
∵AC=BC,
∴点D与点E,点A与点B关于直线CH对称,
∵A(-3,0)、D(0,4),
∴B(9,0);E(6,4),
故答案为:B(9,0);C(3,8);E(6,4);
(2)①∵A(-3,0),B(9,0),
∴AB=|9+3|=12,
∵点D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,DE=
AB=6,
∵PQ∥BC,
∴当点P、点M在线段DE上时四边形PQBE为平行四边形,
∵AD+DE=5+6=11,P、M运动的速度均为每秒1个单位,
∴当5≤t<11时,四边形PQBE为平行四边形;
∵四边形PQBM为菱形,
∴PQ∥BM,
∵PQ∥BE,
∴M、E重合,
∵DE=6,
∴当t=6时,四边形PQBM为菱形.
故答案为:5≤t<11;t=6;
②由题意得:AC=BC=10,AB=12,DE为△ABC的中位线,
则DE∥AB,DE=6,AD=CD=BE=CE=5
当0<t<5时,点P在AD上,点M在DE上,AP=DM=t,
∵PQ∥BC,
∴∠AQP=∠ABC
∵∠PAQ=∠CAB,
∴△PAQ∽△CAB
∴
=
,即
=
,则AQ=
t,BQ=12-
t,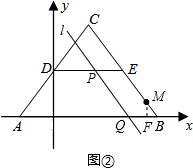
∴S=
(12-
t)•4=-
t+24;
当5≤t≤6时,点P、点M均在DE上,PE=BQ=11-t,
则S=
(11-t)•4=-2t+22;
当6<t<11时,点P在DE上,点M在EB上,则BM=11-t,PE=BQ=11-t,
如图②,过点M作MF⊥AB,垂足为F,则MF=
(11-t)
则S=
(11-t)•
(11-t)=
(11-t)2=
t2-
t+
.
 解:(1)设过点A、D的直线解析式为y=kx+b,
解:(1)设过点A、D的直线解析式为y=kx+b,∵点A(-3,0)、D(0,4)代入得
|
解得
|
∴直线AD的解析式为y=
| 4 |
| 3 |
∴AD=
| (-3)2+42 |
∵点D、E分别是AC、BC的中点,
∴CD=AD=5,
设点C(x,
| 4 |
| 3 |
CD=
x2+(
|
| 5 |
解得x1=3或x2=-3(舍去),
∴C(3,8),
如图①,过点C作CH⊥x轴于点H,则直线CH的解析式为x=3,
∵AC=BC,
∴点D与点E,点A与点B关于直线CH对称,
∵A(-3,0)、D(0,4),
∴B(9,0);E(6,4),
故答案为:B(9,0);C(3,8);E(6,4);
(2)①∵A(-3,0),B(9,0),
∴AB=|9+3|=12,
∵点D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,DE=
| 1 |
| 2 |
∵PQ∥BC,
∴当点P、点M在线段DE上时四边形PQBE为平行四边形,
∵AD+DE=5+6=11,P、M运动的速度均为每秒1个单位,
∴当5≤t<11时,四边形PQBE为平行四边形;
∵四边形PQBM为菱形,
∴PQ∥BM,
∵PQ∥BE,
∴M、E重合,
∵DE=6,
∴当t=6时,四边形PQBM为菱形.
故答案为:5≤t<11;t=6;
②由题意得:AC=BC=10,AB=12,DE为△ABC的中位线,
则DE∥AB,DE=6,AD=CD=BE=CE=5
当0<t<5时,点P在AD上,点M在DE上,AP=DM=t,
∵PQ∥BC,
∴∠AQP=∠ABC
∵∠PAQ=∠CAB,
∴△PAQ∽△CAB
∴
| AP |
| AC |
| AQ |
| AB |
| t |
| 10 |
| AQ |
| 12 |
| 6 |
| 5 |
| 6 |
| 5 |

∴S=
| 1 |
| 2 |
| 6 |
| 5 |
| 12 |
| 5 |
当5≤t≤6时,点P、点M均在DE上,PE=BQ=11-t,
则S=
| 1 |
| 2 |
当6<t<11时,点P在DE上,点M在EB上,则BM=11-t,PE=BQ=11-t,
如图②,过点M作MF⊥AB,垂足为F,则MF=
| 4 |
| 5 |
则S=
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 44 |
| 5 |
| 242 |
| 5 |
点评:本题考查的是相似形综合题,涉及到相似三角形的判定与性质、菱形的判定、平行四边形的判定等相关知识,难度较大.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
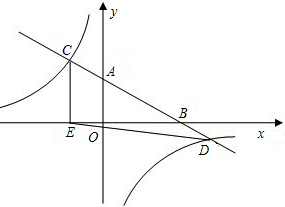 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=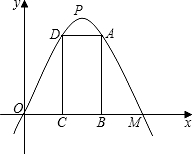 M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上.
M=4,矩形ABCD的边BC在线段OM上,点A、D在抛物线上. ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP. 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(8,0),D点坐标为(0,6),则AC长为 如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )
如图,在平面直角坐标中,点A(2,2),试在x轴上找点P,使△AOP是等腰三角形,那么这样的三角形有( )