题目内容
【题目】如图1，菱形ABCD，AB=4，∠ADC=120o，连接对角线AC、BD交于点O，
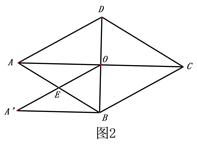
（1）如图2，将△AOD沿DB平移，使点D与点O重合，求平移后的△A′BO与菱形ABCD重合部分的面积.
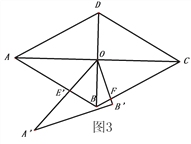
（2）如图3，将△A′BO绕点O逆时针旋转交AB于点E′，交BC于点F，
①求证：BE′+BF=2，
②求出四边形OE′BF的面积.
【答案】(1)
；（2）①2，②
【解析】分析：(1)重合部分是等边三角形，计算出边长即可.
①证明：在图3中，取AB中点E,证明
≌
,即可得到
,
②由①知，在旋转过程60°中始终有≌
四边形
的面积等于
=.
详解：(1)∵四边形为菱形，
∴
∴
为等边三角形
∴
∵AD//
∴
∴
为等边三角形，边长
∴重合部分的面积：
①证明：在图3中，取AB中点E,
由上题知，
∴
又∵
∴≌,
∴
∴,
②由①知，在旋转过程60°中始终有≌
∴四边形的面积等于=.
练习册系列答案
相关题目
