题目内容
 如图在等腰Rt△OBA和Rt△BCD中,∠OBA=∠BCD=90°,点A和点C都在双曲线y=
如图在等腰Rt△OBA和Rt△BCD中,∠OBA=∠BCD=90°,点A和点C都在双曲线y= (k>0)上,求点D的坐标.
(k>0)上,求点D的坐标.
解:过C点作CE⊥BD于E,如图,
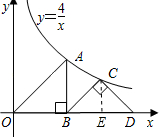
∵△OBA为等腰直角三角形,∠OBA=90°,
∴AB=OB,
设A(a,a),
∴a•a=4,
∴a=2,或a=-2(舍去),即OB=2,
又∵△CBD为等腰直角三角形,∠BCD=90°,
∴CE=BE=DE,
设CE=b,则OE=b+2,OD=2+2b,
∴C点坐标为(b+2,b),
∴(b+2)•b=4,即b2+2b+1=5,
∴(b+1)2=5,
解得b= -1,或b=-
-1,或b=- -1(舍去),
-1(舍去),
∴OD=2( -1)+2=2
-1)+2=2 ,
,
∴点D的坐标为(2 ,0).
,0).
分析:由△OAB为等腰直角三角形,设AB=OB=a,确定A点坐标,代入双曲线解析式求a的值,过C点作CE⊥BD于E,由△CBD为等腰直角三角形,得CE=BE=DE,设CE=b,用表示C点坐标,代入双曲线解析式求b,根据线段关系求D点坐标.
点评:本题考查了反比例函数的综合运用.关键是根据特殊三角形设点的坐标,根据双曲线解析式求点的坐标,根据线段长求点的坐标.

∵△OBA为等腰直角三角形,∠OBA=90°,
∴AB=OB,
设A(a,a),
∴a•a=4,
∴a=2,或a=-2(舍去),即OB=2,
又∵△CBD为等腰直角三角形,∠BCD=90°,
∴CE=BE=DE,
设CE=b,则OE=b+2,OD=2+2b,
∴C点坐标为(b+2,b),
∴(b+2)•b=4,即b2+2b+1=5,
∴(b+1)2=5,
解得b=
 -1,或b=-
-1,或b=- -1(舍去),
-1(舍去),∴OD=2(
 -1)+2=2
-1)+2=2 ,
,∴点D的坐标为(2
 ,0).
,0).分析:由△OAB为等腰直角三角形,设AB=OB=a,确定A点坐标,代入双曲线解析式求a的值,过C点作CE⊥BD于E,由△CBD为等腰直角三角形,得CE=BE=DE,设CE=b,用表示C点坐标,代入双曲线解析式求b,根据线段关系求D点坐标.
点评:本题考查了反比例函数的综合运用.关键是根据特殊三角形设点的坐标,根据双曲线解析式求点的坐标,根据线段长求点的坐标.

练习册系列答案
相关题目

 ),点B的坐标为(6,0).
),点B的坐标为(6,0).

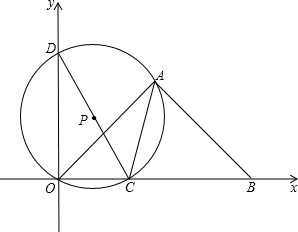 (2013•乐清市模拟)如图,等腰Rt△ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,BO=2,点C(t,0)是线段OB上一动点(不与O,B重合),△OAC的外接圆⊙P与y轴的另一交点为D.
(2013•乐清市模拟)如图,等腰Rt△ABO的斜边OB在x轴上,O是坐标原点,点A在第一象限内,BO=2,点C(t,0)是线段OB上一动点(不与O,B重合),△OAC的外接圆⊙P与y轴的另一交点为D.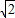 个单位长度的速度运动,点N沿线段OB以每秒1个长度的速度向终点B运动,当N点运动到B点时,M、N同时停止运动,设△PMN的面积为S(S≠0)运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围.
个单位长度的速度运动,点N沿线段OB以每秒1个长度的速度向终点B运动,当N点运动到B点时,M、N同时停止运动,设△PMN的面积为S(S≠0)运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围.