题目内容
12.(1)计算:$(\frac{1}{2}a{b^2}-4{a^2}b)•(-4ab)$
x(y-x)-y(x-y)
(xy)2(-xy)
(2)分解因式:
x3y-2x2y2+xy3
a2+8a+16
(3)解下列方程组:
$\left\{\begin{array}{l}{x=y-2}\\{3x+2y=-1}\end{array}\right.$
$\left\{\begin{array}{l}{\frac{x-1}{2}-\frac{y}{3}=1}\\{2x+y=2}\end{array}\right.$.
分析 (1)原式利用单项式乘以多项式法则计算即可得到结果;原式利用单项式乘以多项式法则计算,去括号合并即可得到结果;原式利用幂的乘方与积的乘方运算法则及单项式乘单项式法则计算即可得到结果;
(2)原式提取公因式,再利用完全平方公式分解即可;原式利用完全平方公式分解即可;
(3)方程组利用代入消元法求出解即可;方程组整理后,利用加减消元法求出解即可.
解答 解:(1)原式=-2a2b3+16a3b2;原式=xy-x2-xy+y2=-x2+y2;原式=-x3y3;
(2)原式=xy(x2-2xy+y2)=xy(x-y)2;原式=(a+4)2;
(3)$\left\{\begin{array}{l}{x=y-2①}\\{3x+2y=-1②}\end{array}\right.$,
把①代入②得:3y-6+2y=-1,即y=1,
把y=1代入①得:x=-1,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$;
方程组整理得:$\left\{\begin{array}{l}{3x-2y=9①}\\{2x+y=2②}\end{array}\right.$,
①+②×2得:7x=13,即x=$\frac{13}{7}$,
把x=$\frac{13}{7}$代入②得:y=-$\frac{12}{7}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{13}{7}}\\{y=-\frac{12}{7}}\end{array}\right.$.
点评 此题考查了整式的混合运算,解二元一次方程组,以及提公因式法与公式法的综合运用,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.数据-1,-2,0,1,2的极差是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.数据8,6,7,9,3,9,5的众数与中位数分别是( )
| A. | 6,7 | B. | 9,5 | C. | 9,7 | D. | 3,5 |
1.下列说法正确的是( )
| A. | 0除以任何数都等于0 | |
| B. | 一个数与它的相反数的商等于-1 | |
| C. | 两个数的商为-1,则这两个数互为相反数 | |
| D. | 两个数相除,商一定小于被除数 |
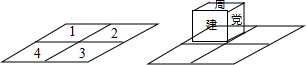 如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.
如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号. 如图,AB∥CD,AF交CD于点E,∠CEF=118°,求∠A的度数.
如图,AB∥CD,AF交CD于点E,∠CEF=118°,求∠A的度数.