题目内容
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 与
与![]() 的平分线交于
的平分线交于![]() 点,连接
点,连接![]() .
.
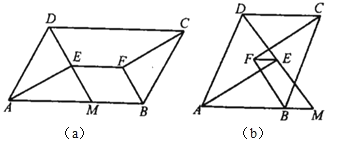
(1)延长![]() 交
交![]() 于
于![]() 点,则图(a)中与线段
点,则图(a)中与线段![]() 一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
(2)![]() 、
、![]() 与
与![]() 之间有怎样的数量关系?为什么?
之间有怎样的数量关系?为什么?
(3)如果将条件“![]() ”改为“
”改为“![]() ”,如图(b)所示,其他条件不变,
”,如图(b)所示,其他条件不变,![]() 、
、![]() 与
与![]() 的关系又如何?直接写出结论.
的关系又如何?直接写出结论.
【答案】(1)与线段![]() 一定相等的线段有
一定相等的线段有![]() 和
和![]() ,理由见解析;(2)EF+BC=AB;(3)EF+AB=BC
,理由见解析;(2)EF+BC=AB;(3)EF+AB=BC
【解析】
(1)根据全等三角形的判定方法,结合题意可得: ![]() ;进而可得
;进而可得
DE=BF,ED=EM;(2)由(1)易得![]() 故
故![]() 进而可得根据平行线的性质可得EF=MB,BC=AD=AM,故有EF+BC=AB;(3)根据题意,利用(2)的方法,易得EFBM是平行四边形,由平行四边形的性质,易得答案.
进而可得根据平行线的性质可得EF=MB,BC=AD=AM,故有EF+BC=AB;(3)根据题意,利用(2)的方法,易得EFBM是平行四边形,由平行四边形的性质,易得答案.
(1)与线段![]() 一定相等的线段有
一定相等的线段有![]() 和
和![]() .
.
∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() 分别平分
分别平分![]() ,∴
,∴![]() ,∴
,∴![]() .同理:
.同理:![]() .
.
∵![]() .∴
.∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)![]() .
.
由(1)易证![]() ,∴
,∴![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
(3)![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目