题目内容
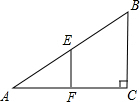 如图,Rt△ABC中,∠C=90°,E、F分别是AB、AC的中点,EF=
如图,Rt△ABC中,∠C=90°,E、F分别是AB、AC的中点,EF=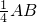 ,那么∠A=________度.
,那么∠A=________度.
30
分析:由E和F分别为AB和AC的中点,得到EF为三角形ABC的中位线,根据三角形的中位线定理可知EF等于BC的一半,由题意可知EF等于AB的 ,从而得到BC等于AB的一半,又因为三角形ABC为直角三角形,根据直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,即可求出角A的度数.
,从而得到BC等于AB的一半,又因为三角形ABC为直角三角形,根据直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,即可求出角A的度数.
解答:∵E、F分别是AB、AC的中点,
∴EF为△ABC的中位线,
∴EF= BC,又EF=
BC,又EF= AB,
AB,
∴BC= AB,又∠C=90°,
AB,又∠C=90°,
∴∠A=30°.
故答案为:30°
点评:此题要求学生掌握三角形中位线定理,中位线定理是一条重要的性质定理,它的结论包括两部分,可以用于证明两条线段的倍(半)关系,也可以用来证明两直线平行.同时要求学生掌握30°角的直角三角形的性质.
分析:由E和F分别为AB和AC的中点,得到EF为三角形ABC的中位线,根据三角形的中位线定理可知EF等于BC的一半,由题意可知EF等于AB的
 ,从而得到BC等于AB的一半,又因为三角形ABC为直角三角形,根据直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,即可求出角A的度数.
,从而得到BC等于AB的一半,又因为三角形ABC为直角三角形,根据直角三角形中一直角边等于斜边的一半,则这条直角边所对的角为30°,即可求出角A的度数.解答:∵E、F分别是AB、AC的中点,
∴EF为△ABC的中位线,
∴EF=
 BC,又EF=
BC,又EF= AB,
AB,∴BC=
 AB,又∠C=90°,
AB,又∠C=90°,∴∠A=30°.
故答案为:30°
点评:此题要求学生掌握三角形中位线定理,中位线定理是一条重要的性质定理,它的结论包括两部分,可以用于证明两条线段的倍(半)关系,也可以用来证明两直线平行.同时要求学生掌握30°角的直角三角形的性质.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.