题目内容
若a>0,b>0,且a<b,则下列式子中成立的是
- A.a2b2>ab
- B.
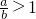
- C.ab>a+b
- D.
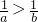
D
分析:根据a>0,b>0,且a<b,可得到b>a>0,再由不等式的基本性质对四个选项进行逐一判断.
解答:∵a>0,b>0,且a<b,∴b>a>0,
A、∵b>a>0,∴b2>0,b2>ab,
∴当a2>1时,a2b2>ab;
当0<a2<1时,a2b2<ab,故本选项错误;
B、∵b>a>0,∴ <1,故本选项错误;
<1,故本选项错误;
C、∵若ab>a+b成立,则b>1+ ,∴此结论无法证明,故本选项错误;
,∴此结论无法证明,故本选项错误;
D、∵b>a>0,∴ >
> ,故本选项正确.
,故本选项正确.
故选D.
点评:本题考查的是不等式的基本性质,熟知不等式的基本性质是解答此题的关键.
分析:根据a>0,b>0,且a<b,可得到b>a>0,再由不等式的基本性质对四个选项进行逐一判断.
解答:∵a>0,b>0,且a<b,∴b>a>0,
A、∵b>a>0,∴b2>0,b2>ab,
∴当a2>1时,a2b2>ab;
当0<a2<1时,a2b2<ab,故本选项错误;
B、∵b>a>0,∴
 <1,故本选项错误;
<1,故本选项错误;C、∵若ab>a+b成立,则b>1+
 ,∴此结论无法证明,故本选项错误;
,∴此结论无法证明,故本选项错误;D、∵b>a>0,∴
 >
> ,故本选项正确.
,故本选项正确.故选D.
点评:本题考查的是不等式的基本性质,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.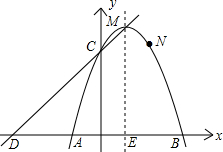 3)三点,且与y轴交于点C.
3)三点,且与y轴交于点C. (2013•天水)如图在平面直角坐标系xOy中,函数y=
(2013•天水)如图在平面直角坐标系xOy中,函数y=