题目内容
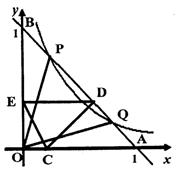
如图,己知双曲线y=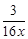 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(1)求△OPQ的面积.
(2)试说明:△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点,CA=a(0<a<1),CD⊥AB于D,DE⊥OB于E.
①a为何值时,CE=AC?
②线段OA上是否存在点C,使CE∥AB?若存在这样的点,请求出点C的坐标:若不存在,请说明理由.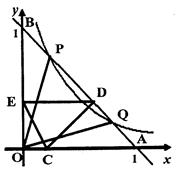
解:(1)∵A(1,0)B(0,1)
∴OB=OA,∠OBA=∠OAB,直线AB的解析式为y=-x+1
∵双曲线 (x>0)与经过点A,B的直线交于P、Q两点
(x>0)与经过点A,B的直线交于P、Q两点
∴

∵
∴
(2) 由(1)得

∵A(1,0)B(0,1)
∴PB=AQ
∵OB=OA,∠OBA=∠OAB
∴△OAQ≌△OBP
(3)①解:作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,
∴
在直角三角形EOC中,
若CE=AC,则
∴
解之得 或
或
∵0<a<1
∴
②若CE∥AB,则有∠ECO=∠OEC=∠B=∠A=45°
∴OE=OC=1-a
作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,
∴
∴
解之得
∴
解析

练习册系列答案
相关题目
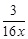 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.