题目内容
19.原点O是△ABC和△A′B′C′的位似中心,点A(2,0)与点A′(-1,0)是对应点,△A′B′C′的面积是3,则△ABC的面积是12.分析 利用位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,ky),进而求出k的值,即可得出答案.
解答 解:∵原点O是△ABC和△A′B′C′的位似中心,点A(2,0)与点A′(-1,0)是对应点,
∴△ABC和△A′B′C′的位似比为:2:1,则面积比为:4:1,
∵△A′B′C′的面积是3,
∴△ABC的面积是:12.
故答案为:12.
点评 此题主要考查了位似变换的性质,正确理解位似与相似的关系,由关于原点位似的两个图形对应点坐标之间的关系得出相似比是解题的关键.

练习册系列答案
相关题目
3. 若有理数a、b在数轴上的位置如图所示,则下列各式中成立的是( )
若有理数a、b在数轴上的位置如图所示,则下列各式中成立的是( )
 若有理数a、b在数轴上的位置如图所示,则下列各式中成立的是( )
若有理数a、b在数轴上的位置如图所示,则下列各式中成立的是( )| A. | a+b<0 | B. | a-b>0 | C. | |a|<|b| | D. | ab>0 |
7.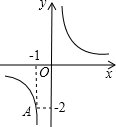 如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
 如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )
如图,反比例函数y=$\frac{k}{x}$的图象经过A(-1,-2),则以下说法错误的是( )| A. | k=2 | B. | 图象也经过点B(2,1) | ||
| C. | 若x<-1时,则y<-2 | D. | x>0,y随x的增大而减小 |
 小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英就获胜,否则小丽获胜(红色+蓝色=紫色).
小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英就获胜,否则小丽获胜(红色+蓝色=紫色). 如图,在方格纸中每个小正方形的顶点称为“格点”,且每个小方格都是边长为1的正方形,已知直线AB经过格点A、B.
如图,在方格纸中每个小正方形的顶点称为“格点”,且每个小方格都是边长为1的正方形,已知直线AB经过格点A、B.