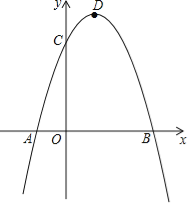
题目内容
【题目】如图，已知第一象限的点A在反比例函数y＝
上，过点A作AB⊥AO交x轴于点B，∠AOB＝30°，将△AOB绕点O逆时针旋转120°，点B的对应点B恰好落在反比例函数y＝
上，则k的值为（ ）
A.﹣4
B.﹣
C.﹣2D.﹣
【答案】B
【解析】
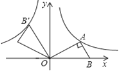
过点B
作
轴的垂线垂足为C，过点
作轴的垂线垂足为D，设点的坐标为
根据反比例函数的解析式和含
角的直角三角形
得出点的坐标，再通过解特殊角度直角三角形得出
的值，再根据旋转得出
，然后证明
，根据全等得出
的值，即可得出点B的坐标，把点B的坐标代入反比例函数解析式即可求得k的值.
过点B作轴的垂线垂足为C，过点作轴的垂线垂足为D，如下图所示：
设点的坐标为，
∵
∴
∴
又∵
∴解得
或
∵点在第一象限
∴不符合题意舍去，
∴点的坐标为
，
∴
∴
∵△AOB绕点O逆时针旋转120°
∴
∴
∴
∴
在
和
中
∴
∴
∵点B旋转后落在第二象限
∴点B的坐标为
∴
解得：
故选：B.
练习册系列答案
相关题目
【题目】攀枝花得天独厚，气候宜人，农产品资源极为丰富，其中晚熟芒果远销北上广等大城市．某水果店购进一批优质晚熟芒果，进价为10元/千克，售价不低于15元/千克，且不超过40元/每千克，根据销售情况，发现该芒果在一天内的销售量
（千克）与该天的售价
（元/千克）之间的数量满足如下表所示的一次函数关系．
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
（1）某天这种芒果售价为28元/千克．求当天该芒果的销售量
（2）设某天销售这种芒果获利
元，写出与售价之间的函数关系式．如果水果店该天获利400元，那么这天芒果的售价为多少元？
