Question

仔细想一想，完成下面的说理过程．
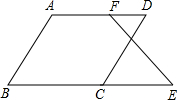
如图，已知AB∥CD，∠B=∠D
求证：∠E=∠DFE．
证明：∵AB∥CD （已知　），
∴∠B+∠________=180°________
又∵∠B=∠D（已知 ）
∴∠D+∠BCD=180°________
∴________
∴∠E=∠DFE________．

Answer 1

BCD    （两直线平行，同旁内角互补）    等量代换    AD∥BC（同旁内角互补，两直线平行）    两直线平行，内错角相等
分析：本题主要根据平行线的判定和性质来填写原因．
解答：证明：∵AB∥CD （已知），
∴∠B+∠BCD=180°（两直线平行，同旁内角互补 ），
又∵∠B=∠D（已知），
∴∠D+∠BCD=180°（等量代换），
∴AD∥BC （同旁内角互补，两直线平行），
∴∠E=∠DFE（两直线平行，内错角相等）．
故答案为 BCD；两直线平行，同旁内角互补；等量代换；AD∥BC （同旁内角互补，两直线平行）；两直线平行，内错角相等．
点评：本题主要考查了平行线的性质和判定．解题的关键是分清角的位置关系，注意性质和判定的联系与区别．