Question

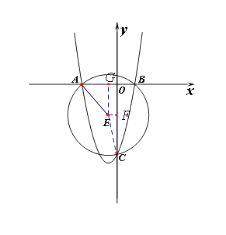
【题目】如图，二次函数y=x2-2mx+8m的图象与x轴交于A、B两点（点A在点B的左边且OA≠OB),交y轴于点C，且经过点（m，9m）,⊙E过A、B、C三点。

（1）求这条抛物线的解析式；

（2）求点E的坐标；

（3）过抛物线上一点P（点P不与B、C重合）作PQ⊥x轴于点Q，是否存在这样的点P使△PBQ和△BOC相似？如果存在，求出点P的坐标；如果不存在，说明理由

Answer 1

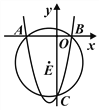
【答案】（1）y=x2+2x-8（2）（-1，-）（3）（-8，40），（-，-），（-，-）

【解析】分析：（1）把代入解析式，得：，解这个方程可求出m的值；

（2）分别令y=0和x=0，求出OA，OB，OC及AB的长，过点作轴于点,轴于点,连接，AE,设OF=GE=a,根据 ，列方过程求出a的值，从而求出点E的坐标；

（3）设点P(a, a2+2a-8)， 则，然后分∽时和∽时两种情况，列比例式求出a的值，从而求出点P的坐标.

详解：（1）把代入解析式，得：

解得：（舍去）

∴

（2）由（1）可得：，当时，;

∵点A在点B的左边 ∴ ，

∴，

当时，，

∴

过点作轴于点,轴于点,连接，,

则 ，

设，则，

在中，，

在中，

，

∵ ，

∴ ，

解得： ，

∴ ；

（3）设点，

则，

a.当∽时，

，即，

解得：（舍去）；

（舍去）； ，

∴ ；

b.当∽时，

，即，

解得：（舍去），； ，

∴； ；

综上所述，点的坐标为：，，