题目内容
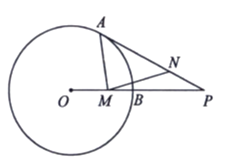
【题目】如图,点![]() 是⊙
是⊙![]() 外一点,
外一点,![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 交⊙
交⊙![]() 于点
于点![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,若
上的动点,若![]() ,
,![]() ,则
,则![]() 的最小值为________.
的最小值为________.
【答案】![]()
【解析】
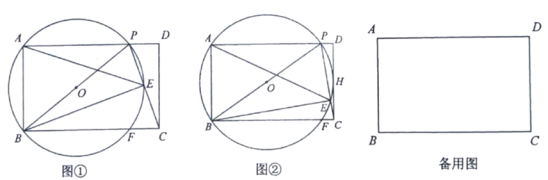
延长PO交⊙![]() 于Q,过点A作AA'⊥OP于C,过A'作A'N⊥AP于N,延长PB交⊙
于Q,过点A作AA'⊥OP于C,过A'作A'N⊥AP于N,延长PB交⊙![]() 于Q,根据切割线定理,得到
于Q,根据切割线定理,得到![]() ,先求出圆的半径,再求出
,先求出圆的半径,再求出![]() ,由
,由![]() 和
和![]() 求出AC,2AC= AA',AN=
求出AC,2AC= AA',AN=![]() ,求出AN,即AM=MN的最小值;
,求出AN,即AM=MN的最小值;
延长PO交⊙![]() 于Q,过点A作AA'⊥OP于C,过A'作AN⊥AP于N,延长PB交⊙
于Q,过点A作AA'⊥OP于C,过A'作AN⊥AP于N,延长PB交⊙![]() 于Q,设⊙
于Q,设⊙![]() 半径为r,
半径为r,

根据切割线定理得,![]() ,
,
∴![]() ,
,
∴r=3;
∴OA=3,OP=5;
∴![]() ;
;
∵AA'⊥OP,
∴![]() °,
°,
∴![]() P+
P+![]() PAA'=90°,
PAA'=90°,![]() 2+
2+![]() PAA'=90°,
PAA'=90°,![]() 1+
1+![]() PAA'=90°,
PAA'=90°,
即![]() 1=
1=![]() 2=
2=![]() P,
P,
∴![]() ,
,
∴![]() ,
,
∴AC=![]() ,
,
∴AA'=![]() ,
,
又![]() ,
,
∴AN=![]() .
.
∴AM+MN的最小值为:![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】(阅读)x与代数式x2+2x﹣1的部分对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
x2+2x﹣1 | … | 2 | ﹣1 | ﹣2 | ﹣1 | 2 | … |
可知:当x=﹣3时,x2+2x﹣1=2>0,当x=﹣2时,x2+2x﹣1=﹣1<0,所以方程x2+2x﹣1=0的一个解在﹣3和﹣2之间.
(理解)(1)方程x2+2x﹣1=0的另一个解在两个连续整数 和 之间.
(应用)(2)若关于x的一元二次方程﹣x2+2x+m=0的一个解在1和2之间,求m的取值范围.