��Ŀ����
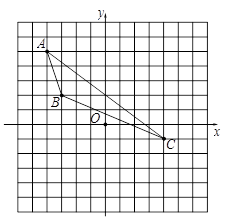
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���![]() �Ķ���
�Ķ���![]() ������ԭ�㣬��
������ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ֱ�Ϊ�ı���
�ֱ�Ϊ�ı���![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() �ӵ�
�ӵ�![]() ��ʼ����ÿ��1����λ���ȵ��ٶ���
��ʼ����ÿ��1����λ���ȵ��ٶ���![]() ·�����е�
·�����е�![]() �����˶�������
�����˶�������![]() ��
��![]() �㿪ʼ����ÿ��������λ���ȵ��ٶ���
�㿪ʼ����ÿ��������λ���ȵ��ٶ���![]() ·�����յ�
·�����յ�![]() �����˶�����
�����˶�����![]() ͬʱ��
ͬʱ��![]() �������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��
�������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��![]() ����
����![]() ����
����![]() �����Ϊ
�����Ϊ![]() .
.
��1����գ�![]() �ij��� ��
�ij��� ��![]() �ij��� ��
�ij��� ��
��2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ʱ�����
ʱ�����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��4����![]() ����ֱ��д����ʱ
����ֱ��д����ʱ![]() ��ֵ.
��ֵ.

���𰸡�(1)10��6����2��S=6����3��y=![]() ��(4)8��
��(4)8��![]() ��
��![]() .
.
��������
�������������![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ɵ�OA=6,OB=8,���ݹ��ɶ����������AB=10������C��CM
���ɵ�OA=6,OB=8,���ݹ��ɶ����������AB=10������C��CM![]() y���ڵ�M���ɵ�
y���ڵ�M���ɵ�![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ɵ� BM=4,CM=2
���ɵ� BM=4,CM=2![]() ,���ɹ��ɶ��������BC=6����2������C��CE
,���ɹ��ɶ��������BC=6����2������C��CE![]() x���ڵ�E���ɵ�
x���ڵ�E���ɵ�![]() ������Ϊ
������Ϊ![]() ���ɵ�CE=4,OE=2
���ɵ�CE=4,OE=2![]() ,��Rt��CEO�У����ݹ��ɶ��������OC=6,��t=3ʱ����N���C�غϣ�OM=3������CM���ɵ�NE=CE=4,����
,��Rt��CEO�У����ݹ��ɶ��������OC=6,��t=3ʱ����N���C�غϣ�OM=3������CM���ɵ�NE=CE=4,����![]() ,��S=6����3����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t������N��NG
,��S=6����3����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t������N��NG![]() y���ڵ�G������C��CF
y���ڵ�G������C��CF![]() y���ڵ�F���ɵ�F(0��4)������OF=4,OB=8,������BGN=��BFC=90�������ж�NG
y���ڵ�F���ɵ�F(0��4)������OF=4,OB=8,������BGN=��BFC=90�������ж�NG![]() CF������
CF������![]() ,��
,��![]() ,���BG=8-
,���BG=8-![]() �����ɵ�y =
�����ɵ�y =![]() ����4��������M���߶�OA�ϣ�N���߶�OC��������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���·�������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���Ϸ����������tֵ����.
����4��������M���߶�OA�ϣ�N���߶�OC��������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���·�������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���Ϸ����������tֵ����.
���������
(1)10��6��
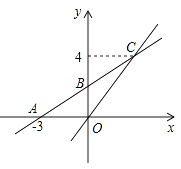
��2����ͼ1������C��CE![]() x���ڵ�E��
x���ڵ�E��
����![]() ������Ϊ
������Ϊ![]() ����CE=4,OE=2
����CE=4,OE=2![]() ,
,
��Rt��CEO��OC=![]() ,
,
��t=3ʱ����N���C�غϣ�OM=3������CM��
��NE=CE=4,
��![]() ,
,
��S=6.
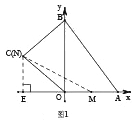
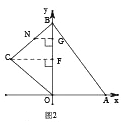
��3����ͼ2����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t��
����N��NG![]() y���ڵ�G������C��CF
y���ڵ�G������C��CF![]() y���ڵ�F����F(0��4)
y���ڵ�F����F(0��4)
��OF=4,OB=8,
��BF=8-4=4
�ߡ�BGN=��BFC=90����
��NG![]() CF
CF
��![]() ,��
,��![]() ,
,
���BG=8-![]() ��
��
��y=OB-BG=8-(8-![]() )=
)=![]()
(4)8��![]() ��
��![]() .
.