题目内容
 如图,四边形OABC是矩形,点O是平面直角坐标系的原点,点A、C分别在x、y轴上,点B的坐标是(3,4),则直线AC的函数表达式是( )
如图,四边形OABC是矩形,点O是平面直角坐标系的原点,点A、C分别在x、y轴上,点B的坐标是(3,4),则直线AC的函数表达式是( )A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=-
|
分析:根据B的坐标可确定A和C的坐标,进而根据待定系数法可求出AC的函数表达式.
解答:解:∵点B的坐标是(3,4),
∴可得A(3,0),C(0,4),
设AC的函数表达式是y=kx+b,
则
,
∴函数关系式为:y=-
x+4.
故选B.
∴可得A(3,0),C(0,4),
设AC的函数表达式是y=kx+b,
则
|
|
∴函数关系式为:y=-
| 4 |
| 3 |
故选B.
点评:本题考查理解平面直角坐标系中点与坐标的意义对应关系,会根据两点的坐标求直线的方程.

练习册系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.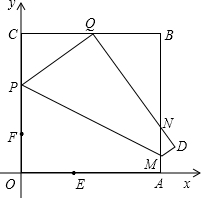
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数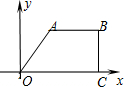 是( )
是( )