题目内容
 如图中,A、B两点的坐标分别为(2,3)、(4,1),
如图中,A、B两点的坐标分别为(2,3)、(4,1),(1)求△ABO的面积.
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′,求△O′A′B′的3个顶点的坐标.
分析:(1)把△ABO放在一个矩形里面,用矩形COED的面积-△ACO的面积-△ABD的面积-△BEO的面积即可算出△ABO的面积;
(2)根据点的坐标平移的规律,用A、B、O的坐标的纵坐标分别减去3即可.
(2)根据点的坐标平移的规律,用A、B、O的坐标的纵坐标分别减去3即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
S△ABO=3×4-
×3×2-
×4×1-
×2×2=5;
(2)A′(2,0),B′(4,-2),O′(0,-3).
 解:(1)如图所示:
解:(1)如图所示:S△ABO=3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)A′(2,0),B′(4,-2),O′(0,-3).
点评:此题主要考查了点的平移,以及求三角形的面积,当计算一个三角形的面积时,可以把它放在一个矩形里,然后用矩形的面积减去周围三角形的面积.

练习册系列答案
相关题目
 矩形OABC在平面直角坐标系中的位置如图所示,AC两点的坐标分别为A(6,0),C(0,3),直线
矩形OABC在平面直角坐标系中的位置如图所示,AC两点的坐标分别为A(6,0),C(0,3),直线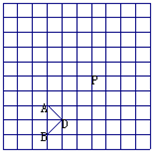 如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形.如图中的△ABD称为格点△ABD.
如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形.如图中的△ABD称为格点△ABD. 与BC相交于D.
与BC相交于D.
 经过D、A两点, 试确定此抛物线的解析式
经过D、A两点, 试确定此抛物线的解析式 轴上方(2)中抛物线上一点, 求
轴上方(2)中抛物线上一点, 求 面积的最大值;
面积的最大值; 相似, 求符合条件的Q点的坐标.
相似, 求符合条件的Q点的坐标. 如图中,A、B两点的坐标分别为(2,3)、(4,1),
如图中,A、B两点的坐标分别为(2,3)、(4,1),