题目内容
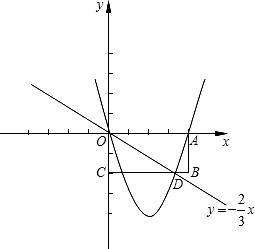
 矩形OABC在平面直角坐标系中的位置如图所示,AC两点的坐标分别为A(6,0),C(0,3),直线y=-
矩形OABC在平面直角坐标系中的位置如图所示,AC两点的坐标分别为A(6,0),C(0,3),直线y=-| 3 |
| 4 |
| 9 |
| 2 |
(1)求点D的坐标;
(2)若上抛物线y=ax2+bx(a≠0)经过A,D两点,试确定此抛物线的解析式;
(3)设(2)中的抛物线的对称轴与直线AD交点M,点P为对称轴上一动点,以P、A、M为顶点的三角形与△ABD相似,求符合条件的所有点P的坐标.
分析:(1)有题目所给信息可以知道,BC线上所有的点的纵坐标都是3,又有D在直线y=-
x+
上,代入后求解可以得出答案.
(2)A、D,两点坐标已知,把它们代入二次函数解析式中,得出两个二元一次方程,联立求解可以得出答案.
(3)由题目分析可以知道∠B=90°,以P、A、M为顶点的三角形与△ABD相似,所以应有∠APM、∠AMP或者∠MAP等于90°,很明显∠AMP不可能等于90°,所以有两种情况.
| 3 |
| 4 |
| 9 |
| 2 |
(2)A、D,两点坐标已知,把它们代入二次函数解析式中,得出两个二元一次方程,联立求解可以得出答案.
(3)由题目分析可以知道∠B=90°,以P、A、M为顶点的三角形与△ABD相似,所以应有∠APM、∠AMP或者∠MAP等于90°,很明显∠AMP不可能等于90°,所以有两种情况.
解答:解:(1)∵四边形OABC为矩形,C(0,3)
∴BC∥OA,点D的纵坐标为3.
∵直线y=-
x+
与BC边相交于点D,∴-
x+
=3.
∴x=2,故点D的坐标为(2,3)
(2)∵若抛物线y=ax2+bx经过A(6,0)、D(2,3)两点,
∴
解得:
∴抛物线的解析式为y=-
x2+
x.

(3)∵抛物线y=-
x2+
x的对称轴为x=3,
设对称轴x=3与x轴交于点P1,∴BA∥MP1,∴∠BAD=∠AMP1.
①∵∠AP1M=∠ABD=90°,∴△ABD∽△MP1A.
∴P1(3,0).
②当∠MAP2=∠ABD=90°时,△ABD∽△MAP2.
∴∠AP2M=∠ADB
∵AP1=AB,∠AP1P2=∠ABD=90°,
∴△AP1P2≌△ABD
∴P1P2=BD=4.
∵点P2在第四象限,∴P2(3,-4).
答:符合条件的点P有两个,P1(3,0)、P2(3,-4).
∴BC∥OA,点D的纵坐标为3.
∵直线y=-
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
∴x=2,故点D的坐标为(2,3)
(2)∵若抛物线y=ax2+bx经过A(6,0)、D(2,3)两点,
∴
|
解得:
|
| 3 |
| 8 |
| 9 |
| 4 |

(3)∵抛物线y=-
| 3 |
| 8 |
| 9 |
| 4 |
设对称轴x=3与x轴交于点P1,∴BA∥MP1,∴∠BAD=∠AMP1.
①∵∠AP1M=∠ABD=90°,∴△ABD∽△MP1A.
∴P1(3,0).
②当∠MAP2=∠ABD=90°时,△ABD∽△MAP2.
∴∠AP2M=∠ADB
∵AP1=AB,∠AP1P2=∠ABD=90°,
∴△AP1P2≌△ABD
∴P1P2=BD=4.
∵点P2在第四象限,∴P2(3,-4).
答:符合条件的点P有两个,P1(3,0)、P2(3,-4).
点评:本题主要考查了二次函数的实际应用,以及三角形的性质等相关知识,属于综合类题目.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 的坐标(0,-2),直线y=-
的坐标(0,-2),直线y=-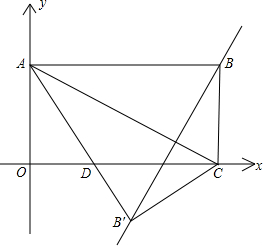 如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足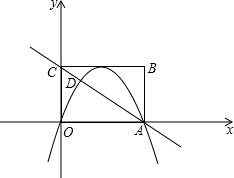 (2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
(2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D. (2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.
(2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.