Question

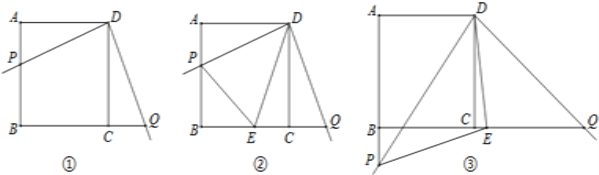
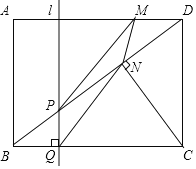
【题目】如图，在矩形ABCD中，CD＝3cm，BC＝4cm，连接BD，并过点C作CN⊥BD，垂足为N，直线l垂直BC，分别交BD、BC于点P、Q．直线l从AB出发，以每秒1cm的速度沿BC方向匀速运动到CD为止；点M沿线段DA以每秒1cm的速度由点D向点A匀速运动，到点A为止，直线1与点M同时出发，设运动时间为t秒（t＞0）．

（1）线段CN＝　 　；

（2）连接PM和QN，当四边形MPQN为平行四边形时，求t的值；

（3）在整个运动过程中，当t为何值时△PMN的面积取得最大值，最大值是多少？

Answer 1

【答案】（1）；（2）t＝；（3）t＝4时，△PMN的面积取得最大值，最大值为．

【解析】

（1）由矩形的性质和勾股定理可求BD的长，由三角形的面积公式可求CN的长；

（2）由勾股定理可求DN的长，通过证明△DMN∽△DAB，可得，可得DM的值，即可求t的值；

（3）分两种情况讨论，利用三角形面积公式列出△PMN的面积与t的关系式，可求△PMN的面积的最大值．

解：（1）∵四边形ABCD是矩形

∴BC＝AD＝4cm，∠BCD＝90°＝∠A，

∴BD＝＝5cm，

∵S△BCD＝BCCD＝BDCN

∴CN＝

故答案为：

（2）在Rt△CDN中，DN＝＝

∵四边形MPQN为平行四边形时

∴PQ∥MN，且PQ⊥BC，AD∥BC

∴MN⊥AD

∴MN∥AB

∴△DMN∽△DAB

∴

即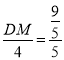

∴DM＝cm

∴t＝

（3）∵BD＝5，DN＝

∴BN＝

如图，过点M作MH⊥BD于点H，

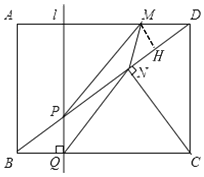
∵sin∠MDH＝sin∠BDA＝

∴

∴MH＝t

当0＜t＜

∵BQ＝t，

∴BP＝t，

∴PN＝BD﹣BP﹣DN＝5﹣﹣t＝﹣t

∴S△PMN＝×PN×MH＝×t×（﹣t）＝﹣t2+t

∴当t＝s时，S△PMN有最大值，且最大值为，

当t＝s时，点P与点N重合，点P，点N，点M不构成三角形；

当＜t≤4时，如图，

∴PN＝BP﹣BN＝t﹣

∴S△PMN＝×PN×MH＝×t×（t﹣）＝t2﹣t

当＜t≤4时，S△PMN随t的增大而增大，

∴当t＝4时，S△PMN最大值为，

∵＞

∴综上所述：t＝4时，△PMN的面积取得最大值，最大值为．